Google Earth Voyager Story: The Geometry of City Planning, Part 2

Why are so many cities laid out in grids? One reason is that straight-line grids take advantage of the fact that the shortest distance between two points is a line. But why are city grids made up of parallel and perpendicular lines?

What are the geometric properties of parallel and perpendicular lines that make these grids ideal for organizing a city? In this investigation we'll look at the properties of these lines and we'll visit different cities around the world to explore these properties.

To see the Google Earth version of this lesson go to this link. (Best viewed in Chrome.)

To see the complete collection of Google Earth Voyager Stories from Media4Math, go to this link.

1. Parallel and Perpendicular Lines

This video activity uses the geometry tools from the TI-Nspire to explore parallel and perpendicular lines. You can adapt this activity using other geometry tools. For example, use the Desmos geometry tools, www.desmos.com/geometry.

2. The Reason Rectangular Grids Are Used

This video summarizes why rectangular grids are used.

This illustration shows three different ways of getting from point A to point B. Verify that each path is identical in length. Let each square in the grid be 1 unit of length. How long are the three different paths?

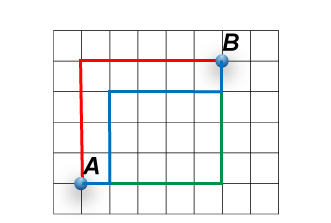
You just saw how three different paths that led from Point A to Point B had the same distance. Now here's a more challenging question: What are the total number of paths possible from A to B?

This is no longer a geometry question, but one involving permutations and combinations. But the answer to the question will bring us back to the geometry of city planning.

In the illustration above, to get from Point A to Point B involves a combination of movements north (N) and east (E). Here is one combination of movements:

N N N N E E E E E

There are four steps north and five steps east, for a total of nine steps. What we want is the combination of the four N's and five E's to get to the total number of possible paths. We get:

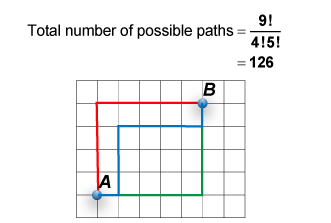
If you were standing at Point A and wanted to get to Point B, you have 126 different ways of getting there! Now imagine that Point A is an intersection in your downtown area. Furthermore, suppose there are a total of 50 pedestrians going from Point A to Point B. This large crowd of people don't have to take the same path. In fact, the 126 different paths means that just a handful of people are on any given path.

Imagine this on a grand scale, with thousands of pedestrians making their way through a downtown center. The rectangular grid plan offers freedom of movement because all paths are equal. This is where the geometry of city plans creates a metropolitan area that can accomodate millions of people.

3. Additional Properties of Parallel and Perpendicular Lines (Optional)

An additional example involving parallel lines involves transversals, or lines that intersect the parallel lines at an angle. You'll see examples of these transversals with some city plans. For example, the street grid for Washington, DC, has a basic rectangular grid that also includes diagonal roads that are equivalent to transversals intersecting parallel lines.