Lesson Plan: Graphing Linear Functions

Lesson Summary

In this lesson, students will delve into the methods of graphing linear functions, enhancing their understanding of the relationship between algebraic equations and their graphical representations. The lesson focuses on:

Graphing linear functions using various methods, including plotting points, utilizing the slope-intercept form, and applying transformations.
Interpreting the meaning of slope and y-intercept from a graph, enabling students to connect graphical features to real-world contexts.
Identifying the x-intercept and y-intercept of a linear function, which are crucial for understanding the behavior of linear equations.

By the end of this lesson, students will be proficient in graphing linear functions and interpreting their key characteristics.

Lesson Objectives

Graph linear functions using various methods
Interpret the meaning of slope and y-intercept from a graph
Identify the x-intercept and y-intercept of a linear function

Common Core Standards

F.IF.7: Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
F.LE.5: Interpret the parameters in a linear or exponential function in terms of a context.

Prerequisite Skills

Understanding linear functions and equations
Plotting points on the Cartesian coordinate plane

Key Vocabulary

x-intercept: The point where a graph crosses the x-axis, indicating where the output value (y) is zero.
y-intercept: The point where a graph crosses the y-axis, representing the output value when the input (x) is zero.
Slope-Intercept Form: A linear equation expressed as $ y = mx + b $, where $ m $ is the slope and $ b $ is the y-intercept.
Point-Slope Form: A linear equation written as $ y - y_1 = m(x - x_1) $, used to define a line with a known slope passing through a specific point $(x_1, y_1)$.
Increasing Function: A function where the output value increases as the input value increases, indicated by a positive slope.
Decreasing Function: A function where the output value decreases as the input value increases, indicated by a negative slope.
Standard Form: A linear equation presented as $ Ax + By = C $, where $ A $, $ B $, and $ C $ are integers, and $ A $ is non-negative.

Multimedia Resources

Math definitions of terms related to linear equations and functions: https://www.media4math.com/Definitions--LinearFunctions
Video definitions on the topic of linear equations and functions: https://www.media4math.com/MathVideoCollection--LinearFunctionsDefinitions
Math definitions of terms related to functions and relations: https://www.media4math.com/Definitions--FunctionsRelations

Warm Up Activities

Activity 1: Review of Graphing Coordinates

Before graphing linear functions, students will review how to plot points on the coordinate plane using the Desmos Graphing Calculator.

Instructions:

Open the Desmos Graphing Calculator.
Click on the "+" button and select "Table" to create a list of ordered pairs.
Enter the following coordinates into the table:
- (-3, 2)
- (-1, -4)
- (2, 3)
- (4, 0)
Observe how the points are positioned on the graph.
Discuss the x- and y-values of each point and how they relate to the coordinate plane.

By practicing plotting points, students will reinforce their understanding of how linear functions are constructed from ordered pairs.

Activity 2: Review of the Vertical Line Test

The Vertical Line Test helps determine whether a graph represents a function. In this activity, students will review how the test works and apply it to different graphs.

Instructions:

Draw different graphs, including:
- A straight line (e.g., $ y = 2x + 3 $)
- A parabola (e.g., $ y = x^2 - 4 $)
- A circle (e.g., $ x^2 + y^2 = 9 $)
- A vertical line (e.g., $ x = -2 $)
Have students use a ruler or pencil to draw vertical lines at different x-values.
If a vertical line crosses the graph more than once at any point, the relation is not a function.
Discuss why vertical lines fail the test and relate it to the definition of a function.

$ y = 2x + 3 $

Passes

$ y = x^2 - 4 $

Passes

$ x^2 + y^2 = 9 $

Doesn't Pass

$ x = -2 $

Doesn't Pass

This activity reinforces the concept that a function assigns exactly one output for each input.

Activity 1: Review of Slope

Display three linear equations in slope-intercept form:

y = 2x + 4

y = 3x - 7

y = -4x - 9

Ask students to identify the slope and y-intercept for each equation. Have them complete a table like this:

Equation	Slope	y-intercept
y = 2x + 4	2	4
y = 3x - 7	3	-7
y = -4x - 9	-4	-9

Teach

Definitions

Review the following video definitions:

Slope-intercept form: https://www.media4math.com/library/74604/asset-preview
Increasing function: https://www.media4math.com/library/74601/asset-preview
Decreasing function: https://www.media4math.com/library/74602/asset-preview
x-intercept: https://www.media4math.com/library/74609/asset-preview
y-intercept: https://www.media4math.com/library/74608/asset-preview
Point-slope form: https://www.media4math.com/library/74606/asset-preview
Standard form:

Show these videos to explain increasing and decreasing functions. The videos describe these properties in the context of any function, but anchor the discussion to linear functions.

Increasing functions: https://www.media4math.com/library/44909/asset-preview
Decreasing functions: https://www.media4math.com/library/44910/asset-preview

Concept Development

Graphing a linear function involves understanding key components such as slope, y-intercept, and different equation forms. The most common form of a linear equation is the slope-intercept form:

\[ y = mx + b \]

$ m $ represents the slope, which describes the steepness and direction of the line.
$ b $ represents the y-intercept, the point where the line crosses the y-axis.

Some linear equations are given in standard form:

\[ Ax + By = C \]

To graph these equations, we convert them into slope-intercept form by solving for $ y $.
The slope can be found using $ m = -\frac{A}{B} $ and the y-intercept using $ b = \frac{C}{B} $.

Use multiple representations to teach graphing linear functions:

Algebraic Representation

Show these equivalent linear equations but written in these forms:

Slope-intercept form: y = -x +1
Standard form: x + y = 1
Point-slope form: y-1 = (-x - 0)

Use this Desmos activity to explore these equivalent forms and explore others:

https://www.desmos.com/calculator/w5spiazzqr

Review this real-world application to generate an equation in standard form:

https://www.media4math.com/library/21416/asset-preview

Review how to convert from standard form to slope-intercept form:

https://www.media4math.com/library/42998/asset-preview

Finally review a step-by-step procedure for the point-slope form:

https://www.media4math.com/library/74306/asset-preview

Graphical Representation

Use this slide show to demonstrate graphing linear functions in slope-intercept form:

https://www.media4math.com/library/slideshow/math-examples-slope-intercept-form

Tabular Representation

Use this slide show to demonstrate multiple representations of linear functions that includes algebraic, graphical, and tabular:

https://www.media4math.com/library/slideshow/multiple-representations-linear-equations

Verbal Representation

Start with a verbal representation that should be familiar to students:

"There is a linear relationship between the circumference of a circle and its radius. What is the linear function?"

Write the equation: C = k•d.

Ask students what k represents. For those who need help have them find the formula for the circumference of a circle.

Select one of these real-world applications of linear functions and show how to derive the appropriate equation:

Cricket chirps vs. Temperature: https://www.media4math.com/library/slideshow/application-linear-functions-cricket-chirps
Cost vs. time for renting equipment: https://www.media4math.com/library/slideshow/application-linear-functions-cost-vs-time
Distance vs. time: https://www.media4math.com/library/slideshow/application-linear-functions-distance-vs-time

Contextual Representation

Introduce this video, which is an application of linear functions in the context of excercise:

https://www.media4math.com/library/21299/asset-preview

Now, let's explore real-world applications of graphing linear functions.

Examples of Graphing Linear Functions

Example 1: Slope-Intercept Form (Hourly Wage)

Problem: A freelancer earns $25 per hour. Write and graph a function for total earnings over time.

Write the function: $ y = 25x $, where:
- $ x $ = hours worked
- $ y $ = total earnings
- Slope $ m = 25 $ (earns $25 per hour)
- Y-intercept $ b = 0 $ (no earnings before working)
Graph the line with slope 25, starting at (0,0).
Domain: $ x \geq 0 $ (cannot work negative hours).
Range: $ y \geq 0 $ (earnings start at zero and increase).

Example 2: Slope-Intercept Form (Water Tank Filling)

Problem: A water tank contains 50 gallons and fills at a rate of 10 gallons per minute.

Write the function: $ y = 10x + 50 $, where:
- $ x $ = minutes
- $ y $ = water level
- Slope $ m = 10 $ (fills at 10 gallons per minute)
- Y-intercept $ b = 50 $ (initial 50 gallons)
Graph starting at (0,50) and increasing with a slope of 10.
Domain: $ x \geq 0 $ (time cannot be negative).
Range: $ y \geq 50 $ (water level starts at 50 gallons).

Example 3: Slope-Intercept Form (Phone Data Plan)

Problem: A phone company charges a $30 monthly fee plus $5 per GB of data used.

Write the function: $ y = 5x + 30 $, where:
- $ x $ = GB of data used
- $ y $ = total monthly bill
- Slope $ m = 5 $ (cost per GB)
- Y-intercept $ b = 30 $ (base fee)
Graph starting at (0,30) and increasing with a slope of 5.
Domain: $ x \geq 0 $ (data usage cannot be negative).
Range: $ y \geq 30 $ (minimum bill is $30).

Example 4: Standard Form (Car Rental Cost)

Problem: A car rental company charges $40 per day plus a $100 deposit.

Equation in standard form: $ 40x - y = -100 $.
Convert to slope-intercept form:\[ y = 40x + 100 \]
Graph starting at (0,100) with a slope of 40.
Domain: $ x \geq 0 $ (cannot rent negative days).
Range: $ y \geq 100 $ (cost starts at $100).

Example 5: Standard Form (Budgeting)

Problem: A student has $200 to spend on books and school supplies, where books cost $20 each and supplies cost $5 each.

Equation in standard form: $ 20x + 5y = 200 $.
Convert to slope-intercept form:\[ y = -4x + 40 \]
Graph starting at (0,40) with a slope of -4.
Domain: $ x \geq 0 $, $ y \geq 0 $ (cannot buy negative items).

Example 6: Standard Form (Car Depreciation)

Problem: A new car is purchased for $30,000 and loses $2,500 in value each year. Write a function to model the car's depreciation over time.

Write the equation in standard form: \[ 2500x + y = 30000 \]
Convert to slope-intercept form by solving for $ y $:\[ y = -2500x + 30000 \]
Graph starting at $ (0, 30000) $, representing the initial value of the car.
The slope of $ -2500 $ means the car loses $2,500 in value each year.
Domain: $ 0 \leq x \leq 12 $ (assuming the car’s value is tracked for 12 years).
Range: $ 0 \leq y \leq 30000 $ (the car’s value decreases but never becomes negative).

Review

Lesson Summary

In this lesson, students explored different methods for graphing linear functions, including using slope-intercept form and converting from standard form. They learned how to identify key components such as slope, y-intercept, and x-intercept, and how these values influence the graph of a function. The lesson also emphasized real-world applications, demonstrating how linear functions model scenarios like earnings, budgeting, and car depreciation.

Students practiced plotting points, using the slope to find additional points, and interpreting graphs based on context. The lesson reinforced the importance of domain and range in determining reasonable values for different real-world scenarios.

Key Vocabulary

Linear Function: A function that forms a straight line when graphed, represented by the equation $ y = mx + b $.
Slope ($ m $): The rate of change of a function, defined as the ratio of vertical change (rise) to horizontal change (run).
Y-Intercept ($ b $): The point where the function crosses the y-axis, found by setting $ x = 0 $ in the equation.
X-Intercept: The point where the function crosses the x-axis, found by setting $ y = 0 $ and solving for $ x $.
Slope-Intercept Form: The equation of a line written as $ y = mx + b $, where $ m $ is the slope and $ b $ is the y-intercept.
Standard Form: The equation of a line written as $ Ax + By = C $, where $ A $, $ B $, and $ C $ are integers, and $ A $ is non-negative.
Domain: The set of all possible input values ($ x $) for a function, often constrained by real-world scenarios.
Range: The set of all possible output values ($ y $) a function can produce.
Increasing Function: A function where $ y $ increases as $ x $ increases, indicated by a positive slope.
Decreasing Function: A function where $ y $ decreases as $ x $ increases, indicated by a negative slope.
Constant Function: A function with a slope of zero, meaning $ y $ does not change regardless of $ x $.

Have students review the different linear forms using these drag-and-drop activities:

Slope-intercept: https://www.media4math.com/library/4829/asset-preview
Standard form: https://www.media4math.com/library/4830/asset-preview
Point-slope form: https://www.media4math.com/library/4841/asset-preview

Quiz

Answer the following questions.

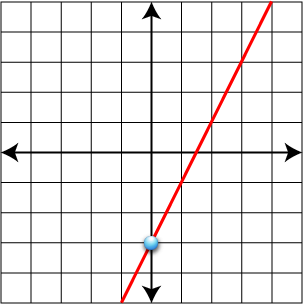
Graph y = 2x - 3
Find the x- and y-intercepts of 3x - 2y = 6
Write the equation of the line passing through (2, 5) with a slope of -1/2
Graph 2x + 3y = 12
Identify the slope and y-intercept of y = -4x + 7
Find the slope of the line passing through (-1, 3) and (4, -2)
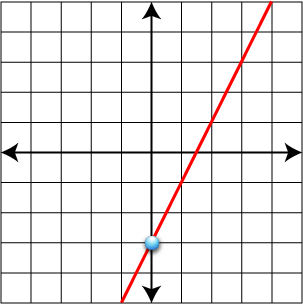
Graph y - 1 = 2(x - 2)
Write the equation of the line with y-intercept 5 and x-intercept -3
Determine if y = -2x + 1 represents an increasing or decreasing function
A company charges a $15 setup fee plus $8 per hour for their service. Write an equation representing the cost (y) in terms of hours (x).

Answer Key

x-intercept: (2, 0), y-intercept: (0, -3)
y - 5 = -1/2(x - 2) or y = -1/2x + 6
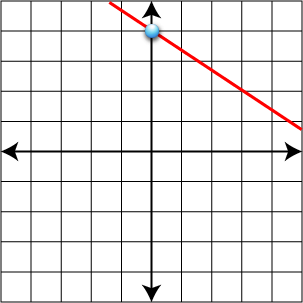
Slope: -4, y-intercept: 7
Slope = -1
y = -5/3x + 5
Decreasing function
y = 8x + 15