
Illustrative Math Alignment: Grade 7 Unit 3
Measuring Circles
Lesson 1: How Well Can You Measure?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
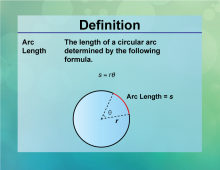
Definition--Circle Concepts--Arc Length | Arc LengthTopicCircles DefinitionAn arc length is the distance along the curved line making up the arc. DescriptionThe arc length is a crucial concept in geometry, particularly when dealing with circles. It is calculated using the formula L = rθ |
Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |
|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Crossword Puzzle--Circles | Interactive Crossword Puzzle--Circles
This interactive crossword puzzle tests knowledge of key terms on the topic of circles. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |
|
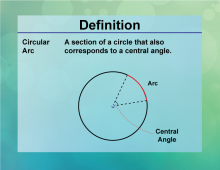
Definition--Circle Concepts--Circular Arc | Circular ArcTopicCircles DefinitionA circular arc is a portion of the circumference of a circle. DescriptionCircular arcs are segments of a circle's circumference, used extensively in design, architecture, and engineering to create curved structures and paths. The length of an arc is determined by the central angle and the circle's radius, calculated using the formula L = rθ |
Definition of a Circle |

|
Definition--Circle Concepts--Circular Arc | Circular ArcTopicCircles DefinitionA circular arc is a portion of the circumference of a circle. DescriptionCircular arcs are segments of a circle's circumference, used extensively in design, architecture, and engineering to create curved structures and paths. The length of an arc is determined by the central angle and the circle's radius, calculated using the formula L = rθ |
Definition of a Circle |

|
Definition--Circle Concepts--Circular Arc | Circular ArcTopicCircles DefinitionA circular arc is a portion of the circumference of a circle. DescriptionCircular arcs are segments of a circle's circumference, used extensively in design, architecture, and engineering to create curved structures and paths. The length of an arc is determined by the central angle and the circle's radius, calculated using the formula L = rθ |
Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Definition--Circle Concepts--Arc Length | Arc LengthTopicCircles DefinitionAn arc length is the distance along the curved line making up the arc. DescriptionThe arc length is a crucial concept in geometry, particularly when dealing with circles. It is calculated using the formula L = rθ |
Definition of a Circle |

|
Definition--Circle Concepts--Arc Length | Arc LengthTopicCircles DefinitionAn arc length is the distance along the curved line making up the arc. DescriptionThe arc length is a crucial concept in geometry, particularly when dealing with circles. It is calculated using the formula L = rθ |
Definition of a Circle |
|
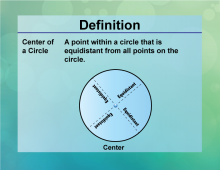
Definition--Circle Concepts--Center of a Circle | Center of a CircleTopicCircles DefinitionThe center of a circle is the point equidistant from all points on the circle. DescriptionThe center of a circle is a pivotal concept in geometry, serving as the reference point from which the radius is measured. It is crucial in defining the circle's position in a plane and is used in various applications such as navigation, where the center can represent a central point of rotation or balance. In mathematical terms, the center is often denoted as the point (h , k) in the Cartesian coordinate system, where all points on the circle satisfy the equation |
Definition of a Circle |

|
Definition--Circle Concepts--Center of a Circle | Center of a CircleTopicCircles DefinitionThe center of a circle is the point equidistant from all points on the circle. DescriptionThe center of a circle is a pivotal concept in geometry, serving as the reference point from which the radius is measured. It is crucial in defining the circle's position in a plane and is used in various applications such as navigation, where the center can represent a central point of rotation or balance. In mathematical terms, the center is often denoted as the point (h , k) in the Cartesian coordinate system, where all points on the circle satisfy the equation |
Definition of a Circle |

|
Definition--Circle Concepts--Center of a Circle | Center of a CircleTopicCircles DefinitionThe center of a circle is the point equidistant from all points on the circle. DescriptionThe center of a circle is a pivotal concept in geometry, serving as the reference point from which the radius is measured. It is crucial in defining the circle's position in a plane and is used in various applications such as navigation, where the center can represent a central point of rotation or balance. In mathematical terms, the center is often denoted as the point (h , k) in the Cartesian coordinate system, where all points on the circle satisfy the equation |
Definition of a Circle |

|
Definition--Geometry Basics--Central Angle | Central AngleTopicGeometry Basics DefinitionAn angle whose vertex is the center of a circle and whose sides are radii. DescriptionA central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. This concept is essential in understanding the properties of circles and the relationships between angles and arcs. For example, the measure of a central angle is equal to the measure of the arc it intercepts. Understanding central angles is important for solving problems related to circle geometry and trigonometry. |
Definition of a Circle |

|
Definition--Geometry Basics--Central Angle | Central AngleTopicGeometry Basics DefinitionAn angle whose vertex is the center of a circle and whose sides are radii. DescriptionA central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. This concept is essential in understanding the properties of circles and the relationships between angles and arcs. For example, the measure of a central angle is equal to the measure of the arc it intercepts. Understanding central angles is important for solving problems related to circle geometry and trigonometry. |
Definition of a Circle |

|
Definition--Geometry Basics--Central Angle | Central AngleTopicGeometry Basics DefinitionAn angle whose vertex is the center of a circle and whose sides are radii. DescriptionA central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. This concept is essential in understanding the properties of circles and the relationships between angles and arcs. For example, the measure of a central angle is equal to the measure of the arc it intercepts. Understanding central angles is important for solving problems related to circle geometry and trigonometry. |
Definition of a Circle |

|
Definition--Geometry Basics--Central Angle | Central AngleTopicGeometry Basics DefinitionAn angle whose vertex is the center of a circle and whose sides are radii. DescriptionA central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. This concept is essential in understanding the properties of circles and the relationships between angles and arcs. For example, the measure of a central angle is equal to the measure of the arc it intercepts. Understanding central angles is important for solving problems related to circle geometry and trigonometry. |
Definition of a Circle |

|
Definition--Geometry Basics--Central Angle | Central AngleTopicGeometry Basics DefinitionAn angle whose vertex is the center of a circle and whose sides are radii. DescriptionA central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. This concept is essential in understanding the properties of circles and the relationships between angles and arcs. For example, the measure of a central angle is equal to the measure of the arc it intercepts. Understanding central angles is important for solving problems related to circle geometry and trigonometry. |
Definition of a Circle |

|
Definition--Geometry Basics--Central Angle | Central AngleTopicGeometry Basics DefinitionAn angle whose vertex is the center of a circle and whose sides are radii. DescriptionA central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle. This concept is essential in understanding the properties of circles and the relationships between angles and arcs. For example, the measure of a central angle is equal to the measure of the arc it intercepts. Understanding central angles is important for solving problems related to circle geometry and trigonometry. |
Definition of a Circle |

|
Math Clip Art Collection: Geometry Concepts | OverviewThis collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres |
Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 1 | VIDEO: Geometry Applications: Circles, 1
TopicCircles DescriptionThis segment discusses the geometry of circles and their cultural and astronomical significance. It introduces concepts such as the center, radius, diameter, chords, and arcs, emphasizing their applications in ancient structures like Pueblo Bonito and Stonehenge. Key vocabulary includes equinox, solstice, radius, and chord. Applications include tracking celestial events and designing circular structures for ceremonial or observational purposes. |
Applications of Circles |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 2 | VIDEO: Geometry Applications: Circles, 2
TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Colosseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Colosseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles | VIDEO: Geometry Applications: Circles
TopicCircles |
Applications of Circles |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
VIDEO: Geometry Applications: Circles, 3 | VIDEO: Geometry Applications: Circles, 3
TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. he video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |

|
Interactive Math Game--Memory Game: Circles | Interactive Math Game--Memory Game: Circles
Use this math game to review circles. This is a Memory-style game in which students must remember the location of pairs of identical images. This is part of a collection of math games and interactives. To see the complete collection of the games, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab. |
Definition of a Circle |