Illustrative Math Alignment: Grade 7 Unit 7

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important.

Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these  figures.

Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms.

In this video tutorial angles are defined. Students are shown how to construct and measure using the Desmos geometry tools. The Desmos geometry tools can be found at www.desmos.com/geometry. . . Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.

In this video tutorial different types of angles are defined, including acute, right, supplementary, and straight angles. Students are shown how to construct these types of angles using the Desmos geometry tools. The Desmos geometry tools can be found at www.desmos.com/geometry. . . Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.

In this video tutorial different types of angles are defined, including adjacent angles, complementary angles, supplementary angles, and vertical angles. Students are shown how to construct these types of angles using the Desmos geometry tools. The Desmos geometry tools can be found at www.desmos.com/geometry. . . Related Resources To see additional resources on this topic click on the Related Resources tab above. Desmos Collection To see the complete collection of Desmos Resources click on this link.

In this video students learn the basics of antiprisms, in the context of New York’s Freedom Tower, which has an antiprism design. They learn the properties of antiprisms, with the focus on those with a square base.

In this video students learn the basics of rectangular prisms, in the context of a New York residential tower: 432 Park Avenue. They learn the properties of rectangular prisms, with and without square bases, and the architectural requirements that influence the use of both types of rectangular prisms.

In this video students study a real-world application of triangular prisms: The Flat Iron Building in New York City. This building is an ideal example of a real-world prism and also provides a tie-in to right triangle geometry. This video describes the geometry of the Flat Iron Building, as well as its architecture. It includes animations that demonstrate the key features of triangular prisms.

In this video students learn the basics of prisms and anti prisms. They learn the properties of triangular prisms, rectangular prisms, triangular antiprisms, and rectangular antiprisms.

Topic

3D Geometry

Topic

3D Geometry

Description

Description: This segment introduces Platonic solids, including tetrahedron, cube, and dodecahedron, emphasizing their congruent edges, vertices, and angles. It connects these geometric figures to both natural and man-made structures, setting the stage for exploring 3D geometry applications.

Topic

3D Geometry

Description

Description: This segment explores pyramids, particularly Mayan and Egyptian structures, to distinguish rectangular and square bases. It discusses the volume of truncated pyramids using proportional relationships and introduces the concept of tiered volume reduction through geometric sequences.

Topic

3D Geometry

Description

Description: This segment examines cylinders, using the Shanghai Tower as a case study. It highlights how adjustments to height and radius affect volume and surface area, demonstrating these principles with geometric calculations and their architectural applications in energy efficiency.

In this program we explore the properties of quadrilaterals. We do this in the context of two real-world applications. In the first, we explore the architecture of Frank Lloyd Wright as an application of squares and rectangles; in particular, we look at his Fallingwater house. In the second application we look at a unique parallelogram-shaped building in Spain, known as the Puerta de Europa. It provides an opportunity to explore the properties of parallelograms and trapezoids.

Stonehenge is best known as a circular structure. But it's the post and lintel construction used that is noteworthy, and this type of construction involves quadrilateral shapes. From the familiar door frames of houses to the majestic entryways of ancient temples, post and lintel construction provides a clear introduction to the nature of quadrilaterals. This segment also describes the key concepts developed throughout the program.

Frank Lloyd Wright’s architectural masterpiece Falling Water is also a stunning assembly of quadrilateral shapes. Some of the rectangular forms in this building seem to defy gravity, as we explore the properties of squares and rectangles that allowed Frank Lloyd Wright to push the envelope of design and structure.

The Puerta de Europa towers in Madrid bring parallelograms front and center. These tilted towers, looking like modern-day towers of Pisa seem to defy gravity, but rely on the stability brought about by its quadrilateral structure. The underlying parallelogram and trapezoidal designs are explored and analyzed.

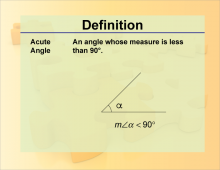
Topic

Angles

Definition

An acute angle is an angle that measures less than 90 degrees.

Topic

Angles

Definition

Adjacent angles are two angles that share a common vertex and side, but do not overlap.

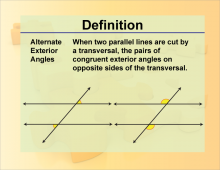
Topic

Angles

Definition

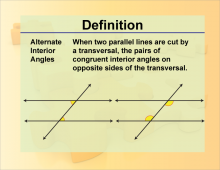
Alternate exterior angles are pairs of angles formed when a transversal crosses two parallel lines, and they lie on opposite sides of the transversal and outside the parallel lines.

Topic

Angles

Definition

Alternate interior angles are pairs of angles formed when a transversal crosses two parallel lines, and they lie on opposite sides of the transversal and inside the parallel lines.

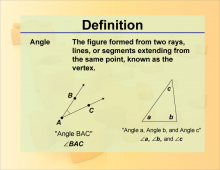
Topic

Angles

Definition

An angle is formed by two rays with a common endpoint, known as the vertex.

Description

Angles are a fundamental concept in geometry, forming the basis for understanding shapes and their properties. They are used in a wide range of applications, from measuring land and constructing buildings to designing machinery and creating art. Angles are measured in degrees or radians, and their understanding is essential for solving problems involving triangles, circles, and other geometric figures. In education, angles are introduced early in the curriculum to develop spatial awareness and geometric reasoning, providing a foundation for more advanced mathematical concepts.

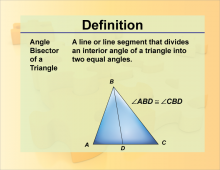
Topic

Angles

Definition

An angle bisector is a line or ray that divides an angle into two equal parts.

Description

Angle bisectors are used in various geometric constructions and proofs, such as constructing the incenter of a triangle, which is the point where the angle bisectors of a triangle intersect. In practical applications, angle bisectors are used in design and architecture to create symmetrical and balanced structures. For students, learning about angle bisectors enhances their understanding of geometric constructions and the properties of angles, contributing to their overall mathematical proficiency.

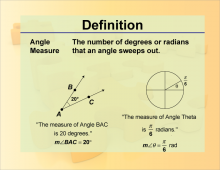
Topic

Angles

Definition

Angle measure refers to the size of an angle, typically expressed in degrees or radians.

Description

Understanding angle measurement is crucial for solving geometric problems and for applications in trigonometry, physics, and engineering. Accurate angle measurement is essential in fields such as surveying, navigation, and construction, where precise calculations are necessary for successful outcomes. In education, mastering angle measurement is a key component of the geometry curriculum, helping students develop skills in spatial reasoning and problem-solving.

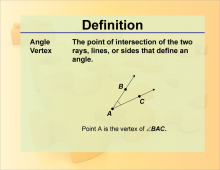
Topic

Angles

Definition

The vertex of an angle is the common endpoint of the two rays that form the angle.

Topic

Angles

Definition

A central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle.

Description

Central angles are important in the study of circles and are used to define arcs and sectors. They are commonly used in problems involving circular motion and in the design of circular objects, such as wheels and gears. In mathematics education, understanding central angles helps students grasp the properties of circles and their applications, forming a basis for more advanced studies in trigonometry and calculus.

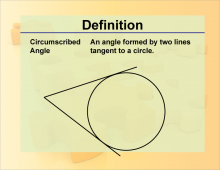
Topic

Angles

Definition

A circumscribed angle is an angle formed outside a circle by two intersecting lines, each tangent to the circle.

Description

Circumscribed angles are used in geometry to study the properties of tangents and their relationships with circles. They are important in problems involving circle theorems and are applied in fields such as architecture and design, where circular shapes are common. For students, learning about circumscribed angles enhances their understanding of circle geometry and the relationships between angles and arcs, contributing to their overall mathematical knowledge.

Topic

Angles

Definition

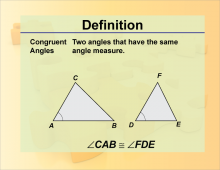
Complementary angles are two angles whose measures add up to 90 degrees.

Topic

Angles

Definition

Congruent angles are angles that have the same measure.

Description

Congruent angles are a key concept in geometry, often used in proving the similarity and congruence of geometric figures. They are essential in understanding the properties of polygons, where congruent angles indicate symmetry and balance. In real-world applications, congruent angles are used in design and engineering to ensure that components are identical and fit together seamlessly. For students, learning about congruent angles enhances their understanding of geometric relationships and proofs, contributing to their overall mathematical proficiency.

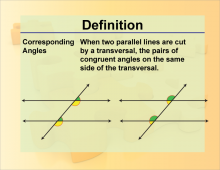
Topic

Angles

Definition

Corresponding angles are pairs of angles that are in similar positions at each intersection where a transversal crosses two lines.

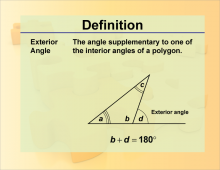
Topic

Angles

Definition

An exterior angle is an angle formed outside a polygon by extending one of its sides.

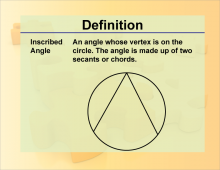
Topic

Angles

Definition

An inscribed angle is an angle formed by two chords in a circle that have a common endpoint.

Description

Inscribed angles are important in the study of circles, where they are used to define arcs and sectors. They are commonly used in problems involving circle theorems and in the design of circular objects, such as wheels and gears. In mathematics education, understanding inscribed angles helps students grasp the properties of circles and their applications, forming a basis for more advanced studies in trigonometry and calculus.

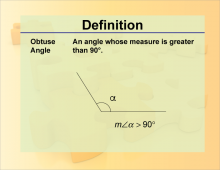
Topic

Angles

Definition

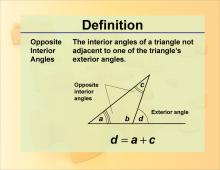
An obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees.

Topic

Angles

Definition

Opposite interior angles are pairs of angles opposite the exterior angle of a triangle. In the case of parallel lines cut by a transversal, they are congruent. 

Topic

Angles

Definition

A reflex angle is an angle that measures more than 180 degrees but less than 360 degrees.

Description

Reflex angles are often encountered in the study of rotations and circular motion, where they are used to describe angles that extend beyond a straight line. They are important in fields such as physics and engineering, where understanding rotations and angular measurements is crucial. In mathematics education, reflex angles help students develop a comprehensive understanding of angle measurement and classification, contributing to their overall geometric reasoning and problem-solving abilities.

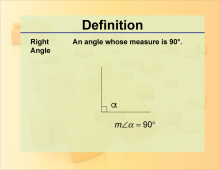
Topic

Angles

Definition

A right angle is an angle that measures exactly 90 degrees.

Description

Right angles are fundamental in geometry and are often used as a reference for measuring other angles. They are commonly found in various geometric shapes and real-world structures, such as squares, rectangles, and buildings. In real-world applications, right angles are essential in construction and design, where they ensure that elements are perpendicular and aligned correctly. In education, understanding right angles is crucial for learning about perpendicularity and the properties of geometric figures, forming a basis for more advanced mathematical concepts.

Topic

Angles

Definition

A straight angle is an angle that measures exactly 180 degrees.

Description

Straight angles are used to describe angles that form a straight line, often encountered in the study of linear relationships and transformations. They are important in fields such as physics and engineering, where understanding linear motion and alignment is crucial. In mathematics education, straight angles help students develop a comprehensive understanding of angle measurement and classification, contributing to their overall geometric reasoning and problem-solving abilities.

Topic

Angles

Definition

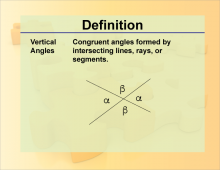
Supplementary angles are two angles whose measures add up to 180 degrees.

Topic

Angles

Definition

Vertical angles are pairs of opposite angles formed by two intersecting lines, and they are equal in measure.

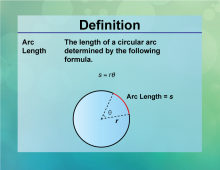
Topic

Circles

Definition

An arc length is the distance along the curved line making up the arc.

Description

The arc length is a crucial concept in geometry, particularly when dealing with circles. It is calculated using the formula 

L = rθ

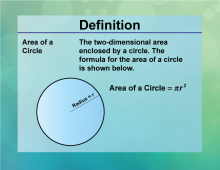
Topic

Circles

Definition

The area of a circle is the space contained within its circumference, calculated as 

A = πr2

Description

The area of a circle is a fundamental concept in geometry, representing the space enclosed by the circle's boundary. This concept is widely applicable in fields such as physics, engineering, and design, where understanding the area is crucial for tasks like calculating material quantities or designing circular components. The formula 

A = πr2 

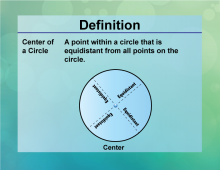
Topic

Circles

Definition

The center of a circle is the point equidistant from all points on the circle.

Description

The center of a circle is a pivotal concept in geometry, serving as the reference point from which the radius is measured. It is crucial in defining the circle's position in a plane and is used in various applications such as navigation, where the center can represent a central point of rotation or balance. In mathematical terms, the center is often denoted as the point (h , k) in the Cartesian coordinate system, where all points on the circle satisfy the equation 

Topic

Circles

Definition

A chord is a line segment with both endpoints on the circle.