
Illustrative Math Alignment: Grade 8 Unit 1
Rigid Transformations and Congruence
Lesson 13: Congruence
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Clip Art Collection: Triangles |
OverviewThis collection aggregates all the math clip art around the topic of Triangles. There are a total of 14 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.To download the full set of these resources, click on this link.
|
Applications of Coordinate Geometry, Applications of Triangles, Definition of a Triangle and Right Triangles |
|
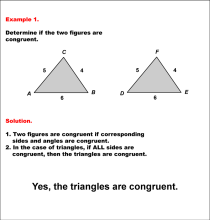
Math Examples Collection: Analyzing Congruent Shapes | OverviewThe Media4Math collection on Analyzing Congruent Shapes provides a comprehensive set of math examples designed to deepen students' understanding of congruence. These examples cover a range of skills, starting with basic shape identification and progressing to more complex applications of congruence in transformations and geometric reasoning. By presenting examples that increase in complexity, students are guided step-by-step to master the concept of congruence in a structured way. |
Definition of a Triangle |

|
Closed Captioned Video: Geometry Applications: Triangles, 2 | Closed Captioned Video: Geometry Applications: Triangles, 2TopicTriangles |
Definition of a Triangle and Applications of Triangles |
|
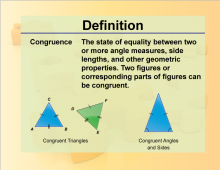
Definition--Geometry Basics--Congruence | CongruenceTopicGeometry Basics DefinitionCongruence refers to figures or shapes that have the same size and shape. DescriptionCongruence is a fundamental concept in geometry, indicating that two figures are identical in form and dimensions. This concept is essential for understanding geometric transformations and proving the properties of shapes. For instance, two triangles are congruent if their corresponding sides and angles are equal. Congruence is used in various real-world applications, such as engineering and architecture, to ensure precision and accuracy in design and construction. |
Definition of Transformations |
|
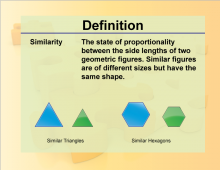
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |
|
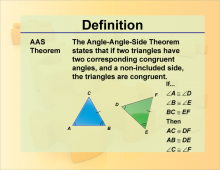
Definition--Theorems and Postulates--AAS Theorem | Definition--Theorems and Postulates--AAS Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
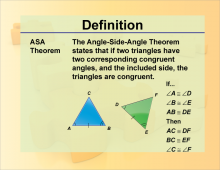
Definition--Theorems and Postulates--ASA Theorem | Definition--Theorems and Postulates--ASA Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of an Angle |

|
Definition--Theorems and Postulates--HL Theorem | Definition--Theorems and Postulates--HL Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Right Triangles |
|
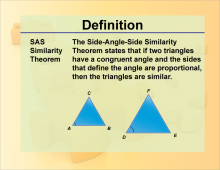
Definition--Theorems and Postulates--SAS Similarity Theorem | Definition--Theorems and Postulates--SAS Similarity Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
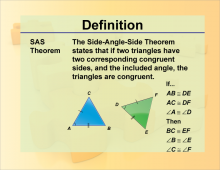
Definition--Theorems and Postulates--SAS Theorem | Definition--Theorems and Postulates--SAS Theorem
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
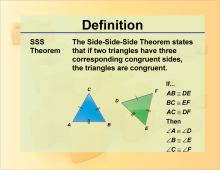
Definition--Theorems and Postulates--SSS Postulate | Definition--Theorems and Postulates--SSS Postulate
This is part of a collection of definitions of geometric theorems and postulates. |
Definition of a Triangle |
|
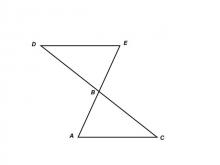
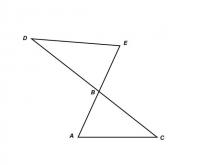
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
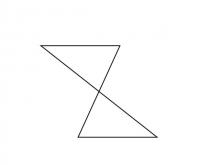
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
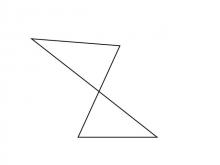
|
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
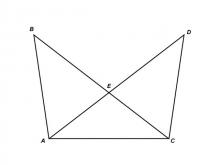
|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
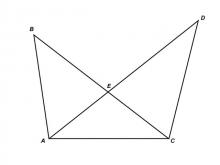
|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
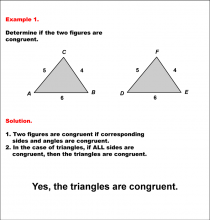
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
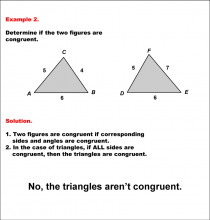
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
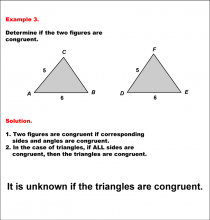
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Video Transcript: Geometry Applications: Triangles | Video Transcript: Geometry Applications: Triangles
This is the transcript for the video of same title. Video contents: In this program we explore the properties of triangle. We do this in the context of two real-world applications. In the first, we explore the triangular trusses in the Eiffel Tower and in the process learn about key properties of triangles. In the second application, we look at right-triangle-shaped sails on sail boat and why these are the ideal shape for efficient sailing. |
Applications of Triangles |

|
Video Transcript: Geometry Applications: Triangles, Segment 1: Introduction | Video Transcript: Geometry Applications: Triangles, Segment 1: Introduction
This is the transcript for the video of same title. Video contents: The Bank of China building in Hong Kong is a dramatic example of triangular support. The notion of triangular trusses is introduced, along with the key concepts developed in the rest of the program. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Triangles |

|
Video Transcript: Geometry Applications: Triangles, Segment 2: Triangles | Video Transcript: Geometry Applications: Triangles, Segment 2: Triangles
This is the transcript for the video of same title. Video contents: The Eiffel Tower includes quite a number of exposed triangular trusses. The properties of triangles are used to explore and explain the frequent use of triangular trusses in many building. In particular, isosceles and equilateral triangular trusses are explored. In addition triangle postulates and similarity are explored and analyzed. |
Applications of Triangles |

|
VIDEO: Geometry Applications: Triangles, 2 | VIDEO: Geometry Applications: Triangles, 2
TopicTriangles |
Applications of Triangles |