Illustrative Math Alignment: Grade 8 Unit 1
Rigid Transformations and Congruence
Lesson 8: Rotation Patterns
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Examples Collection: Transformations | OverviewThe Transformations collection on Media4Math offers a comprehensive set of 56 math examples, providing educators with a rich resource for teaching geometric transformations. This collection covers a wide range of skills and concepts related to transformations, including translations, reflections, rotations, and dilations. |
Definition of Transformations |
|
Math Video Collection: Geometry Applications Video Series: Transformations |
OverviewThis collection aggregates all the math videos and resources in this series: Geometry Applications Video Series: Transformations. There are a total of 12 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
Applications of Transformations and Definition of Transformations |
|
Closed Captioned Video: Geometry Applications: Transformations | Closed Captioned Video: Geometry Applications: TransformationsTopicTransformations |
Definition of Transformations and Applications of Transformations |
|
Closed Captioned Video: Geometry Applications: Transformations, 1 | Closed Captioned Video: Geometry Applications: Transformations, 1TopicTransformations DescriptionExplores translations and rotations in motion, using roller coasters as an example. Key concepts include displacement vectors, magnitude, and direction, modeled geometrically and computationally for practical applications in physics and engineering. In this video, you will explore the fascinating applications of transformations in real-world scenarios. These mathematical concepts are central to understanding geometric principles and their practical applications in various fields. |
Definition of Transformations and Applications of Transformations |
|
Closed Captioned Video: Geometry Applications: Transformations, 2 | Closed Captioned Video: Geometry Applications: Transformations, 2TopicTransformations DescriptionThis segment applies 3D translations to logistics, focusing on container arrangement in shipping. Using coordinate systems, it demonstrates efficiency in loading/unloading cargo, leveraging geometric organization and data sorting methods for real-world impact. In this video, you will explore the fascinating applications of transformations in real-world scenarios. These mathematical concepts are central to understanding geometric principles and their practical applications in various fields. |
Definition of Transformations and Applications of Transformations |
|
Closed Captioned Video: Geometry Applications: Transformations, 3 | Closed Captioned Video: Geometry Applications: Transformations, 3TopicTransformations DescriptionAnalyzes observatory designs and their use of rotational and reflective symmetry for astronomical viewing. The segment models celestial movements and applies rotational geometry concepts to optimize the structure’s functionality. In this video, you will explore the fascinating applications of transformations in real-world scenarios. These mathematical concepts are central to understanding geometric principles and their practical applications in various fields. |
Definition of Transformations and Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter A | Math Clip Art--Bilateral Symmetry of the Letter ATopicGeometry Concepts DescriptionThis image illustrates the concept of bilateral symmetry using the capital letter A. Bilateral symmetry occurs when an object can be divided into two identical halves by a single line, creating mirror images on either side. In this case, the letter A demonstrates perfect bilateral symmetry along a vertical axis drawn through its center. The left side of the letter is an exact mirror image of the right side. This symmetry is evident in the equal angles of the letter's legs and the centered position of the crossbar. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter H | Math Clip Art--Bilateral Symmetry of the Letter HTopicGeometry Concepts DescriptionThis image showcases the bilateral symmetry of the capital letter H. Bilateral symmetry is present when an object can be divided into two identical halves by a single line, creating mirror images on each side. The letter H exhibits bilateral symmetry along both vertical and horizontal axes. A vertical line through the center of the H divides it into identical left and right halves, while a horizontal line through its center creates identical top and bottom halves. This dual symmetry makes H one of the most symmetrical letters in the alphabet. This image shows the vertical line of symmetry. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter I | Math Clip Art--Bilateral Symmetry of the Letter ITopicGeometry Concepts DescriptionThis image demonstrates the bilateral symmetry of the capital letter I. Bilateral symmetry occurs when an object can be divided into two identical halves by a single line, creating mirror images on either side. The letter I displays bilateral symmetry along both vertical and horizontal axes. A vertical line through its center creates identical left and right halves, while a horizontal line produces identical top and bottom halves. This makes I, like H, one of the most symmetrical letters in the alphabet. This image shows the vertical line of symmetry. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter M | Math Clip Art--Bilateral Symmetry of the Letter MTopicGeometry Concepts DescriptionThis image illustrates the bilateral symmetry of the capital letter M. Bilateral symmetry is present when an object can be divided into two identical halves by a single line, creating mirror images on each side. The letter M demonstrates bilateral symmetry along a vertical axis drawn through its center. The left half of the M is a perfect mirror image of the right half, with the central peak serving as the axis of symmetry. This symmetry is evident in the equal angles and lengths of the letter's diagonal strokes. |
Applications of Transformations |
|
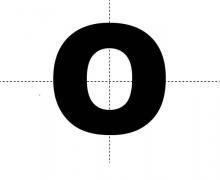
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter O | Math Clip Art--Bilateral Symmetry of the Letter OTopicGeometry Concepts DescriptionThis image showcases the bilateral symmetry of the capital letter O. Bilateral symmetry occurs when an object can be divided into two identical halves by a single line, creating mirror images on either side. The letter O is unique among alphabet letters as it possesses infinite lines of symmetry if drawn as a perfect circle. Any straight line passing through the center of the O will divide it into two identical halves, demonstrating both vertical and horizontal bilateral symmetry, as well as diagonal symmetry. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter T | Math Clip Art--Bilateral Symmetry of the Letter TTopicGeometry Concepts DescriptionThis image illustrates the bilateral symmetry of the capital letter T. Bilateral symmetry occurs when an object can be divided into two identical halves by a single line, creating mirror images on either side. The letter T demonstrates perfect bilateral symmetry along a vertical axis drawn through its center. The left side of the vertical stem is an exact mirror image of the right side, and the horizontal bar is equally divided by this axis. This symmetry is evident in the equal length of the horizontal bar on either side of the vertical stem. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter U | Math Clip Art--Bilateral Symmetry of the Letter UTopicGeometry Concepts DescriptionThis image showcases the bilateral symmetry of the capital letter U. Bilateral symmetry is present when an object can be divided into two identical halves by a single line, creating mirror images on each side. The letter U exhibits bilateral symmetry along a vertical axis drawn through its center. The left side of the U is a perfect mirror image of the right side, with both vertical strokes being of equal length and the curved bottom perfectly symmetrical. This symmetry is evident in the equal distance between the vertical strokes and the center line at any given height. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter V | Math Clip Art--Bilateral Symmetry of the Letter VTopicGeometry Concepts DescriptionThis image demonstrates the bilateral symmetry of the capital letter V. Bilateral symmetry occurs when an object can be divided into two identical halves by a single line, creating mirror images on either side. The letter V displays perfect bilateral symmetry along a vertical axis drawn through its center. The left diagonal stroke is an exact mirror image of the right diagonal stroke, with both meeting at a point at the bottom. This symmetry is evident in the equal angles formed by each stroke with the vertical axis. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter W | Math Clip Art--Bilateral Symmetry of the Letter WTopicGeometry Concepts DescriptionThis image illustrates the bilateral symmetry of the capital letter W. Bilateral symmetry is present when an object can be divided into two identical halves by a single line, creating mirror images on each side. The letter W demonstrates bilateral symmetry along a vertical axis drawn through its center. The left half of the W is a perfect mirror image of the right half, with the central peak serving as the axis of symmetry. This symmetry is evident in the equal angles and lengths of the letter's diagonal strokes on either side of the central axis. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter X | Math Clip Art--Bilateral Symmetry of the Letter XTopicGeometry Concepts DescriptionThis image showcases the bilateral symmetry of the capital letter X. Bilateral symmetry occurs when an object can be divided into two identical halves by a single line, creating mirror images on either side. The letter X is unique in that it exhibits bilateral symmetry along both vertical and horizontal axes. A vertical line through the center of the X divides it into identical left and right halves, while a horizontal line creates identical top and bottom halves. This dual symmetry makes X one of the most symmetrical letters in the alphabet. This image shows the vertical line of symmetry. |
Applications of Transformations |
|
Math Clip Art--Geometry Concepts--Bilateral Symmetry of the Letter Y | Math Clip Art--Bilateral Symmetry of the Letter YTopicGeometry Concepts DescriptionThis image illustrates the bilateral symmetry of the capital letter Y. Bilateral symmetry is present when an object can be divided into two identical halves by a single line, creating mirror images on each side. The letter Y demonstrates bilateral symmetry along a vertical axis drawn through its center. The upper arms of the Y are mirror images of each other, with the vertical stem extending down from their point of convergence. This symmetry is evident in the equal angles formed by the upper arms with the vertical axis and their equal length. |
Applications of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 1 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 1
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 10 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 10
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 11 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 11
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
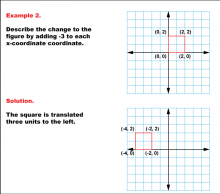
Math Example--Geometric Transformation--Transformations with Coordinates--Example 2 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 2
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
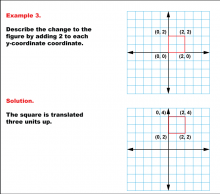
Math Example--Geometric Transformation--Transformations with Coordinates--Example 3 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 3
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 4 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 4
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 5 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 5
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
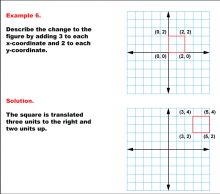
Math Example--Geometric Transformation--Transformations with Coordinates--Example 6 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 6
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
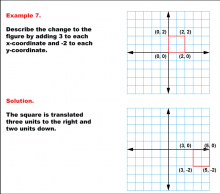
Math Example--Geometric Transformation--Transformations with Coordinates--Example 7 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 7
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 8 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 8
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations with Coordinates--Example 9 | Math Example--Geometric Transformation--Transformations with Coordinates--Example 9
This is part of a collection of math examples that focus on geometric transformations. |
Definition of Transformations |
|
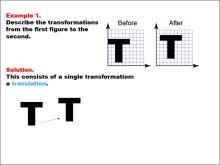
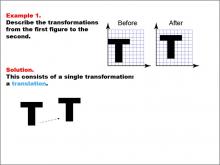
Math Example--Geometric Transformation--Transformations: Example 1 | Math Example--Geometric Transformation--Transformations: Example 1TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two "T" shapes are shown on a grid, labeled "Before" and "After". The "Before" shape on the left is translated to become the "After" shape on the right, illustrating how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
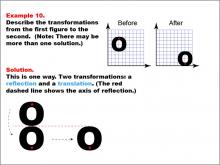
Math Example--Geometric Transformation--Transformations: Example 10 | Math Example--Geometric Transformation--Transformations: Example 10TopicTransformations DescriptionThis example showcases a combination of reflection and translation in geometric transformations. Two circular "O" shapes are displayed on a grid, one labeled "Before" and the other "After". A red dashed line indicates the axis of reflection. The transformation involves first reflecting the shape across this axis and then translating it to a new position. This demonstrates how multiple transformations can be applied in sequence to create more complex movements. |
Definition of Transformations |
|
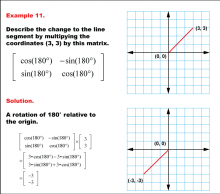
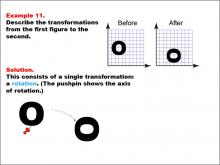
Math Example--Geometric Transformation--Transformations: Example 11 | Math Example--Geometric Transformation--Transformations: Example 11TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. Two circular "O" shapes are shown on a grid, one labeled "Before" and the other "After". The shape undergoes a rotation around a point indicated by a pushpin, which serves as the axis of rotation. This illustrates how an object can change its orientation without altering its size or position relative to the rotation point. |
Definition of Transformations |
|
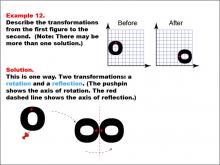
Math Example--Geometric Transformation--Transformations: Example 12 | Math Example--Geometric Transformation--Transformations: Example 12TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. Two circular "O" shapes are displayed on a grid, one labeled "Before" and the other "After". The transformation involves two steps: first, a rotation around a point indicated by a pushpin, which serves as the axis of rotation, followed by a reflection across a red dashed line representing the axis of reflection. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
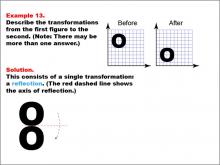
Math Example--Geometric Transformation--Transformations: Example 13 | Math Example--Geometric Transformation--Transformations: Example 13TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. Two grids are shown with the letter "O" before and after a transformation. The "Before" grid has the "O" on the left side, while the "After" grid has it on the right side. A red dashed line indicates the axis of reflection in the middle of the two "O"s. Below, there is a diagram showing the reflection transformation along this axis, illustrating how the shape is flipped across the line while maintaining its size and shape. |
Definition of Transformations |
|
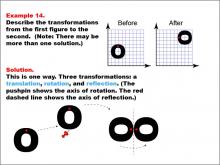
Math Example--Geometric Transformation--Transformations: Example 14 | Math Example--Geometric Transformation--Transformations: Example 14TopicTransformations DescriptionThis example illustrates a complex combination of transformations: translation, rotation, and reflection. Two grids are shown with an "O" shape before and after transformations. The "Before" grid has an "O" with a red dot at its center, while the "After" grid shows the same "O" but rotated and reflected. Below, a step-by-step diagram illustrates three sequential transformations: first, a translation moves the shape, then a rotation turns it around a pushpin (indicating the axis of rotation), and finally, a reflection flips it across a red dashed line. |
Definition of Transformations |
|
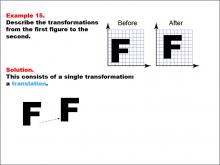
Math Example--Geometric Transformation--Transformations: Example 15 | Math Example--Geometric Transformation--Transformations: Example 15TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two grids are displayed with the letter "F" before and after a transformation. The "Before" grid shows an "F" on the left side, and the "After" grid shows it on the right side. Below, there is an arrow indicating that only a translation occurred between the two positions of the letter, showcasing how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
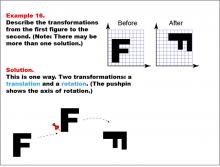
Math Example--Geometric Transformation--Transformations: Example 16 | Math Example--Geometric Transformation--Transformations: Example 16TopicTransformations DescriptionThis example demonstrates a combination of translation and rotation in geometric transformations. Two grids are shown with the letter "F" before and after transformations. The "Before" grid has an upright "F", while the "After" grid shows it rotated 90 degrees clockwise. Below, there is a diagram illustrating two steps: first, a translation moves the shape, then a rotation turns it around a pushpin axis. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations: Example 17 | Math Example--Geometric Transformation--Transformations: Example 17TopicTransformations DescriptionThis example illustrates a combination of reflection and translation in geometric transformations. The image shows a large letter "F" on a grid transforming into a letter "L". The transformation involves two steps: first, a reflection across an axis represented by a red dashed line, and then a translation to a new position. |
Definition of Transformations |
|
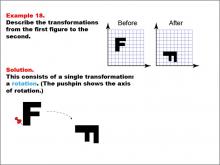
Math Example--Geometric Transformation--Transformations: Example 18 | Math Example--Geometric Transformation--Transformations: Example 18TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows the letter "F" on a grid being rotated to form the same letter in a different orientation. A pushpin indicates the axis of rotation, and an arrow shows the direction of rotation, illustrating how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
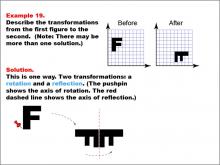
Math Example--Geometric Transformation--Transformations: Example 19 | Math Example--Geometric Transformation--Transformations: Example 19TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image shows the letter "F" being transformed into an upside-down version of itself. This transformation involves two steps: first, a rotation around an axis indicated by a pushpin, followed by a reflection across a line represented by a red dashed line. |
Definition of Transformations |
|
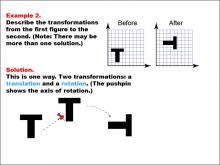
Math Example--Geometric Transformation--Transformations: Example 2 | Math Example--Geometric Transformation--Transformations: Example 2TopicTransformations DescriptionThis example illustrates a combination of transformations: translation and rotation. Two "T" shapes are shown on a grid, labeled "Before" and "After". The shape undergoes a translation (movement) and a rotation, with a pushpin indicating the axis of rotation. This demonstrates how multiple transformations can be applied sequentially to a shape. |
Definition of Transformations |
|
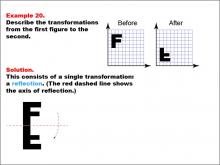
Math Example--Geometric Transformation--Transformations: Example 20 | Math Example--Geometric Transformation--Transformations: Example 20TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows the letter "F" being reflected to form the letter "L". A red dashed line indicates the axis of reflection, illustrating how the letter changes its orientation through this single transformation. This showcases how an object can be flipped over a line while changing its shape and orientation. |
Definition of Transformations |
|
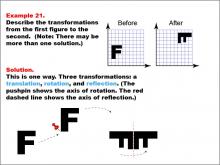
Math Example--Geometric Transformation--Transformations: Example 21 | Math Example--Geometric Transformation--Transformations: Example 21TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows an uppercase letter "F" on a grid labeled "Before" and a transformed version of the letter "F" upside down on another grid labeled "After." Below, there are illustrations showing the three steps of the transformation process. |
Definition of Transformations |
|
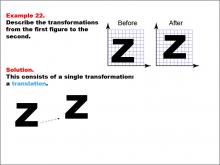
Math Example--Geometric Transformation--Transformations: Example 22 | Math Example--Geometric Transformation--Transformations: Example 22TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and a horizontally shifted version of the same letter on another grid labeled "After." Below, there is an illustration showing just a translation, indicating that the letter "Z" is moved horizontally without any rotation or reflection. |
Definition of Transformations |
|
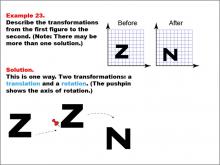
Math Example--Geometric Transformation--Transformations: Example 23 | Math Example--Geometric Transformation--Transformations: Example 23TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and an uppercase letter "N" on another grid labeled "After." Below, there are illustrations showing the two steps of the transformation: first a translation (moving the figure) followed by a rotation (turning the figure). A pushpin indicates the axis of rotation. |
Definition of Transformations |
|
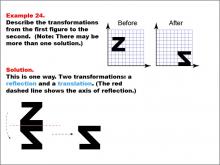
Math Example--Geometric Transformation--Transformations: Example 24 | Math Example--Geometric Transformation--Transformations: Example 24TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows an uppercase letter "Z" on a grid labeled "Before" and a rotated and translated version of the same letter in another position on another grid labeled "After." Below, there are illustrations showing the two steps of the transformation: first, a reflection (flipping the figure across an axis shown by the red dashed line) and then a translation (moving the figure). |
Definition of Transformations |
|
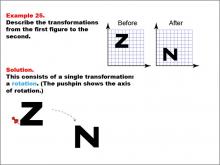
Math Example--Geometric Transformation--Transformations: Example 25 | Math Example--Geometric Transformation--Transformations: Example 25TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows a transformation of the letter "Z" from an upright position to a rotated position resembling "N". The grid background helps visualize the transformation, and a pushpin icon indicates the axis of rotation, illustrating how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
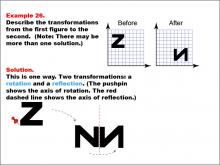
Math Example--Geometric Transformation--Transformations: Example 26 | Math Example--Geometric Transformation--Transformations: Example 26TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image shows a transformation of the letter "Z" into an upside-down "N". A pushpin indicates the axis of rotation, and a red dashed line represents the axis of reflection. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
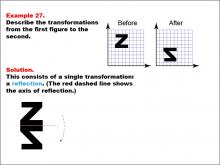
Math Example--Geometric Transformation--Transformations: Example 27 | Math Example--Geometric Transformation--Transformations: Example 27TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows a reflection of the letter "Z" across a horizontal red dashed line, resulting in a backward "Z". The grid background helps visualize the reflection, illustrating how an object can be flipped over a line while maintaining its size and shape but changing its orientation. |
Definition of Transformations |
|
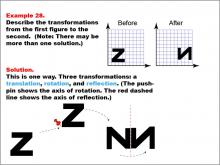
Math Example--Geometric Transformation--Transformations: Example 28 | Math Example--Geometric Transformation--Transformations: Example 28TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows a transformation of the letter "Z" into an upside-down "N". This transformation involves three steps: first, a translation moves the shape, then a rotation turns it (indicated by a pushpin showing the axis of rotation), and finally, a reflection flips it across a red dashed line representing the axis of reflection. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations: Example 29 | Math Example--Geometric Transformation--Transformations: Example 29TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows a "Before" and "After" transformation of a black square on a grid. The square moves horizontally to the right, and a dotted arrow indicates the direction of movement. This showcases how an object can move position without changing its size or orientation. |
Definition of Transformations |
