Illustrative Math Alignment: Grade 8 Unit 2

Dilations, Similarity, and Introducing Slope

Lesson 6: Similarity

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Math Examples Collection: Analyzing Congruent Shapes	Overview The Media4Math collection on Analyzing Congruent Shapes provides a comprehensive set of math examples designed to deepen students' understanding of congruence. These examples cover a range of skills, starting with basic shape identification and progressing to more complex applications of congruence in transformations and geometric reasoning. By presenting examples that increase in complexity, students are guided step-by-step to master the concept of congruence in a structured way.	Definition of a Triangle
Math Examples Collection: Analyzing Similar Shapes	Overview The Analyzing Similar Shapes collection on Media4Math offers a rich set of examples designed to deepen students' understanding of geometric similarity. This collection provides a progression of problems, starting with basic concepts and increasing in complexity to challenge students with diverse skills. Key topics include proportional reasoning, identifying scale factors, and using geometric transformations.	Definition of a Triangle
Math Clip Art Collection: Similarity Transformations	Overview This collection aggregates all the math clip art around the topic of Similarity Transformations. There are a total of 11 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation. To download the full set of these resources, click on this link.	Proportions
Math Clip Art Collection: Triangles	Overview This collection aggregates all the math clip art around the topic of Triangles. There are a total of 14 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation. To download the full set of these resources, click on this link.	Applications of Coordinate Geometry, Applications of Triangles, Definition of a Triangle and Right Triangles
Math Definitions Collection: Geometry	Overview The Geometry Basics collection from Media4Math is an essential resource for educators looking to enhance their students' understanding of fundamental geometric concepts. This comprehensive set includes 58 terms, each presented as a downloadable PNG image card that can be seamlessly integrated into classroom presentations.	Definition of an Angle, Geometric Constructions with Points and Lines, 3-Dimensional Figures, Exploring Coordinate Systems, Definition of a Triangle, Definition of a Point, Definition of a Circle, Definition of Transformations, The Distance Formula, Definition of a Polygon, Definition of a Plane, Definition of a Line, Midpoint Formula, Applications of Polygons, Area and Perimeter of Triangles, Area and Perimeter of Quadrilaterals, Pyramids, Trig Expressions and Identities, Right Triangles, Definition of a Quadrilateral, Applications of Points and Lines and Proportions
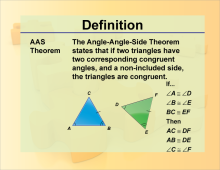
Math Definitions Collection: Geometry Theorems and Postulates	Overview This collection aggregates all the definition image cards around the topic of Theorems and Postulates terms and vocabulary. There are a total of 18 terms. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.	Definition of a Triangle, Definition of an Angle, Right Triangles and Definition of a Line
Math Clip Art Collection: Geometry Concepts	Overview This collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres	Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons
Closed Captioned Video: Geometry Applications: Triangles, 2	Closed Captioned Video: Geometry Applications: Triangles, 2 Topic Triangles	Definition of a Triangle and Applications of Triangles
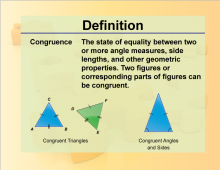
Definition--Geometry Basics--Congruence	Congruence Topic Geometry Basics Definition Congruence refers to figures or shapes that have the same size and shape. Description Congruence is a fundamental concept in geometry, indicating that two figures are identical in form and dimensions. This concept is essential for understanding geometric transformations and proving the properties of shapes. For instance, two triangles are congruent if their corresponding sides and angles are equal. Congruence is used in various real-world applications, such as engineering and architecture, to ensure precision and accuracy in design and construction.	Definition of Transformations
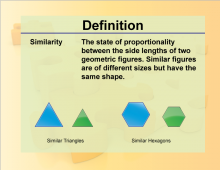
Definition--Geometry Basics--Similarity	Similarity Topic Geometry Basics Definition Similarity refers to figures that have the same shape but not necessarily the same size. Description Similarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures.	Proportions
Definition--Geometry Basics--Similarity	Similarity Topic Geometry Basics Definition Similarity refers to figures that have the same shape but not necessarily the same size. Description Similarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures.	Proportions
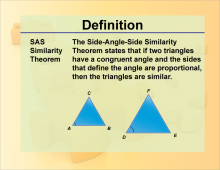
Definition--Theorems and Postulates--SAS Similarity Theorem	Definition--Theorems and Postulates--SAS Similarity Theorem This is part of a collection of definitions of geometric theorems and postulates.	Definition of a Triangle
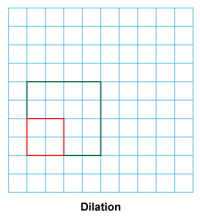
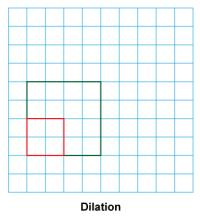
Math Clip Art--Geometry Concepts--Similarity with Transformations--01	Math Clip Art--Similarity with Transformations--01 Topic Geometry Concepts Description This image depicts a square undergoing a dilation transformation. Dilation changes the size of a figure while maintaining its shape, resulting in a similar figure. The scale factor of the dilation determines whether the square is enlarged or reduced. In this transformation, all sides of the square are scaled by the same factor, and all angles remain congruent to the original. This preserves the square's shape while changing its size, demonstrating the concept of similarity in geometry.	Proportions
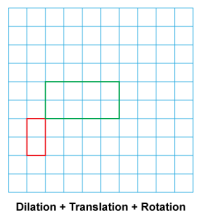
Math Clip Art--Geometry Concepts--Similarity with Transformations--02	Math Clip Art--Similarity with Transformations--02 Topic Geometry Concepts Description This image shows a square undergoing a combination of dilation and translation. The dilation changes the size of the square while maintaining its shape, and the translation moves the dilated square to a new position without changing its size or orientation. This composite transformation demonstrates how multiple transformations can be applied sequentially. The resulting figure is similar to the original square but different in size and position.	Proportions
Math Clip Art--Geometry Concepts--Similarity with Transformations--03	Math Clip Art--Similarity with Transformations--03 Topic Geometry Concepts Description This image illustrates a rectangle undergoing a combination of dilation, translation, and rotation. The dilation changes the size of the rectangle, the translation moves it to a new position, and the rotation changes its orientation. This complex transformation demonstrates how multiple transformations can be combined to create a figure that is similar to the original but different in size, position, and orientation. The resulting figure maintains the proportions of the original rectangle.	Proportions
Math Clip Art--Geometry Concepts--Similarity with Transformations--04	Math Clip Art--Similarity with Transformations--04 Topic Geometry Concepts Description This image shows a rectangle undergoing a combination of dilation and rotation. The dilation changes the size of the rectangle while maintaining its proportions, and the rotation changes its orientation. This transformation demonstrates how a figure can be both resized and reoriented while maintaining its shape. The resulting figure is similar to the original rectangle but different in size and orientation.	Proportions
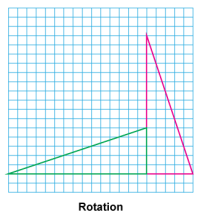
Math Clip Art--Geometry Concepts--Similarity with Transformations--05	Math Clip Art--Similarity with Transformations--05 Topic Geometry Concepts Description This image depicts a triangle undergoing a rotation transformation. The rotation changes the orientation of the triangle without altering its size or shape. This transformation demonstrates how a figure can be moved around a fixed point (the center of rotation) while maintaining its congruence to the original shape. The resulting triangle is identical to the original in all aspects except its orientation.	Proportions
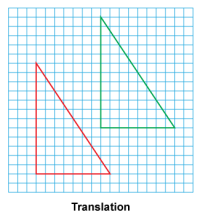
Math Clip Art--Geometry Concepts--Similarity with Transformations--06	Math Clip Art--Similarity with Transformations--06 Topic Geometry Concepts Description This image shows a triangle undergoing a translation transformation. The translation moves the triangle to a new position without changing its size, shape, or orientation. This transformation demonstrates how a figure can be moved in a straight line without any other changes. The resulting triangle is congruent to the original and maintains all its properties, only differing in its position.	Proportions
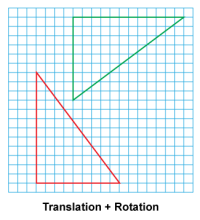
Math Clip Art--Geometry Concepts--Similarity with Transformations--07	Math Clip Art--Similarity with Transformations--07 Topic Geometry Concepts Description This image illustrates a triangle undergoing a combination of translation and rotation. The translation moves the triangle to a new position, and the rotation changes its orientation. This composite transformation demonstrates how multiple transformations can be applied sequentially. The resulting triangle is congruent to the original but different in both position and orientation.	Proportions
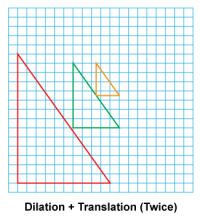
Math Clip Art--Geometry Concepts--Similarity with Transformations--08	Math Clip Art--Similarity with Transformations--08 Topic Geometry Concepts Description This image shows a triangle undergoing a combination of dilation and translation performed twice. The dilation changes the size of the triangle while maintaining its shape, and the translations move it to new positions. This complex transformation demonstrates how multiple transformations can be applied repeatedly. The resulting triangles are similar to the original but differ in size and position.	Proportions
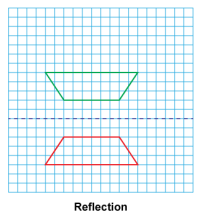
Math Clip Art--Geometry Concepts--Similarity with Transformations--09	Math Clip Art--Similarity with Transformations--09 Topic Geometry Concepts Description This image depicts a trapezoid reflected across a horizontal line. Reflection creates a mirror image of the original figure across a line of reflection. This transformation demonstrates how a figure can be flipped over a line to create its mirror image. The resulting trapezoid is congruent to the original but inverted vertically. Teacher's Script: "Observe how the trapezoid is reflected across the horizontal line. What properties of the trapezoid remain unchanged? How does the orientation of the trapezoid change after reflection? Can you identify the line of reflection?"	Proportions
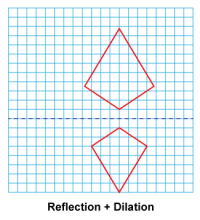
Math Clip Art--Geometry Concepts--Similarity with Transformations--10	Math Clip Art--Similarity with Transformations--10 Topic Geometry Concepts Description This image shows a kite reflected across a horizontal line, followed by a dilation. Reflection creates a mirror image of the original figure across a line of reflection. Dilation changes the size of the original figure but keeps it proportional. This transformation demonstrates how a figure can be flipped over a line to create its mirror image. The resulting kite is similar to the original but inverted vertically.	Proportions
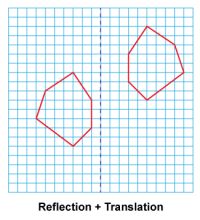
Math Clip Art--Geometry Concepts--Similarity with Transformations--11	Math Clip Art--Similarity with Transformations--11 Topic Geometry Concepts Description This image illustrates an irregular hexagon reflected across a vertical line. Reflection creates a mirror image of the original figure across a line of reflection. This transformation demonstrates how a complex figure can be flipped over a vertical line to create its mirror image. The resulting hexagon is congruent to the original but reversed horizontally.	Proportions
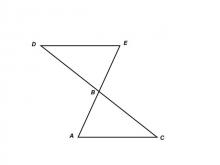
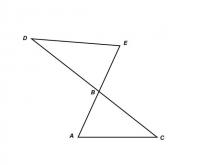
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled	Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
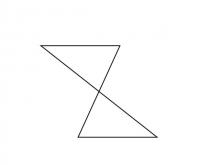
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled	Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled	Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
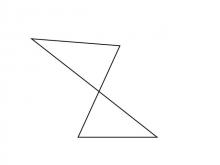
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled	Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
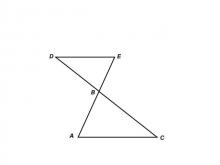
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Similar--Labeled	Math Clip Art--Triangles--Two Triangles Share Vertical Angles Similar--Labeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
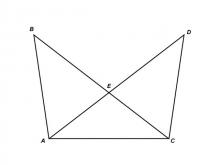
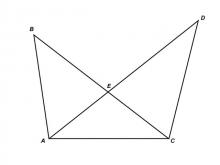
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled	Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled	Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled	Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled	Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled This is from a collection of triangular shapes. They come labeled and unlabeled.	Applications of Triangles
Math Clip Art: Comparing Right Triangles	Math Clip Art: Comparing Right Triangles Use these clip art images and the background grid to test if the right triangles are similar.	Right Triangles
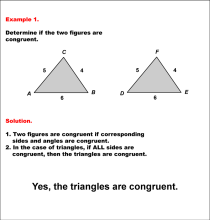
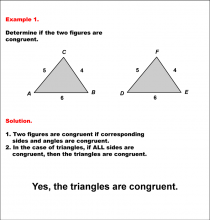
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
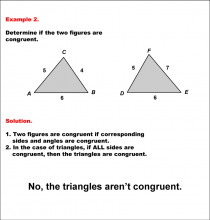
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
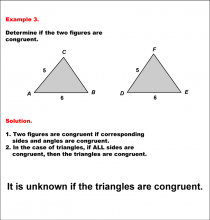
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 Topic Geometric Shapes Description Determine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 Topic Geometric Shapes Description Determine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9	Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 Topic Geometric Shapes Description Determine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence.	Definition of a Triangle
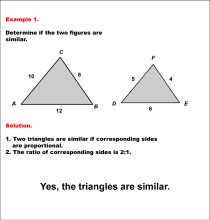
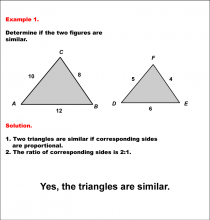
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 4, and 6. Triangles are similar if corresponding sides are proportional. Here, the ratio of corresponding sides is 2:1 (10:5, 8:4, 12:6). Thus, the triangles are similar. Therefore, the answer is Yes, the triangles are similar.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10 Topic Geometric Shapes Description Determine if two right triangles are similar. The triangle on the left has angle 40°, and the other triangle has a 60° angle. For similarity, all corresponding angles must be congruent. The angles in each triangle do not match, so the triangles aren't similar. Therefore, the answer is No, the triangles aren't similar.	Definition of a Triangle
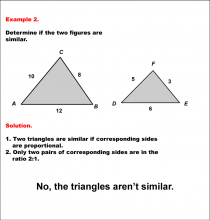
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 3, and 6. Triangles are similar if all corresponding sides are proportional. Only two pairs of sides here have a 2:1 ratio, so the triangles are not similar. Therefore, the answer is No, the triangles arenÕt similar.	Definition of a Triangle
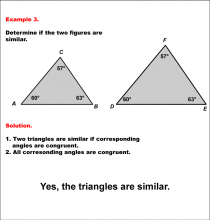
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Both triangles have angles 60°, 57°, and 63°. Triangles are similar if corresponding angles are equal. Since all corresponding angles match, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Triangle ABC has angles 75°, 42°, and an unknown angle, and triangle DEF has angles 75° and 63° and an unknown angles. Triangles are similar if all corresponding angles are congruent. Solving for the unknown angles confirms angle congruency, so the triangles are similar. Therefore, the answer is Yes, the triangles are similar.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5 Topic Geometric Shapes Description Determine if two right triangles, ABC and DEF, are similar. Triangle ABC has angles 90° and 40°, and triangle DEF has angles 90° and 50°. Triangles are similar if all corresponding angles are congruent. Solving reveals congruent corresponding angles. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Triangle ABC has a right angle and an angle of 40°, and triangle DEF has a right angle and 45°. Not all corresponding angles are congruent, so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept.	Definition of a Triangle
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7	Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7 Topic Geometric Shapes Description Determine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 45° angle. Triangles are similar if two pairs of sides are proportional, and the included angle is congruent. The side ratio is 2:1, and both included angles are 45°. Therefore, the answer is Yes, the triangles are similar.	Definition of a Triangle