Illustrative Math Alignment: Grade 6 Unit 3

Turn the Halloween season into an opportunity to do some math activities! In this module, you'll find a clever collection of arithmetic, algebra, and geometry activities.

Temperature is one of the most important measurements that we deal with on a daily basis. Weather, climate, food preparation, health, and other phenomena involve some type of temperature measure. The two most common units of temperature measure are Fahrenheit and Celsius.

There is a linear function that allows you to convert from one unit to another. In this module, you'll learn about this linear function. In fact, students will learn about this function and its inverse.

The module starts with an analysis of Celsius-to-Fahrenheit data. They look at the functional relationship between the variables and develop a linear model using the Desmos graphing calculator. They analyze the properties of this linear function and look at its graph.

Next, students analyze Fahrenheit-to-Celsius data. They also develop a linear function model using the Desmos graphing calculator.

As the size of a circle changes, so does the size of the diameter and that of the circumference. In fact, there is a linear relationship between these two measures. This relationship can be modeled with a linear function. In this module students will study this linear function and examine its properties, including the fact that the slope of this function is π itself.

This is a hands-on module in which students will measure the diameters and circumferences of a number of different containers. This data gathering will lead to graphing the data. From that students develop a linear model using the Desmos graphing tool. Students will see that the relationship between circumference and diameter has to do with π. In fact, the slope of the linear function is π itself.

Rivers twist and turn as they make their way to the sea. Why does this happen and how can this be explained mathematically? In this module we look at the geometry of meandering rivers. In the process we'll discover some fascinating numerical relationships.

Students will learn some basic concepts about the geophysics of how rivers form, but they will focus their analysis on what is called the sinuousity ratio. This is the ratio of the straight-line distance of the river and its meandering distance. This ratio reveals important characteristics of the river. Then, students will develop and examine geometric models involving circular arcs and segments to get a better understanding of the ratio. These models will first involve using a compass and straight edge to model a river. This is followed by an algebraic analysis.

Have you noticed how wrinkled an elephant's skin is? What purpose does it serve and what does math have to do with explaining this phenomenon? Well, the explanation for an elephant's wrinkled skin is almost entirely a math story. 

In this module students explore rational expressions and functions in the context of the ratio of surface area and volume for various three-dimensional figures. Such figures can be used to model the basic shapes of animals.

This ratio reveals a lot about how an animal is able to retain heat or lose it rapidly, depending on the animal's habitat. The geometry of heat transfer also has applications in architecture and design.

What your students will learn:

Overview

Overview

In this real-world application of ratios, students will learn what a ratio is, including ratios with three terms. They will see different ways of writing ratios, including fractions in simplest form. 

a:b     ab     a to b

Two short videos introduce the concept of ratios and each video includes real-world examples of ratios. Then several formative assessments are used to test for understanding.  

Students then look at the application of ratios to the mixing of concrete at a construction site, starting with a video then followed by an assessment.

This lesson can be assigned to individual students or teams of students. The lesson can be completed in about 20 minutes. 

Overview

This collection of definitions on the topic of Ratios, Proportions, and Percents from Media4Math is an invaluable educational resource designed to enhance students' understanding of these fundamental mathematical concepts. This comprehensive collection includes essential terms such as ratio, proportion, percent, rate, unit rate, and scale model.

Overview

Topic

Equations

Description

This segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications.

Topic

Percents

Description

This video applies percents to measure slopes or grades, using ratios for rise over run. Examples include road inclines, ski slopes, and cycling paths. Applications showcase percents in engineering, sports, and transportation, emphasizing their practicality in measuring inclines accurately.

Topic

Percents

Description

The video demonstrates calculating tips and commissions using percentages. Examples include restaurant tips, real estate commissions, and catering costs. Applications focus on service industry calculations and earnings management.

Topic

Percents

Description

This video covers tax calculations for purchases, property, and VAT. Examples include grocery bills, iPad purchases, and real estate property taxes. Applications highlight the importance of understanding tax rates for budgeting and financial management.

Topic

Percents

Description

This video demonstrates solving for the whole when given a percent and a part. Examples include lemonade recipes, mixing paint, and counting UFOs. Techniques involve writing equations using decimals for percents and solving for the unknown total. Key vocabulary includes part, whole, and equation setup, with practical applications in recipes, art, and problem-solving.

Topic

Percents

Description

This video teaches estimation techniques for calculating percents without a calculator. Examples include estimating fish populations, race participants, and cyclists. Visual aids like rectangles partitioned into fractions assist with rounding percents for quick calculations. Applications focus on efficient mental math for real-world approximations.

Topic

Percents

Description

The video explores converting fractions to percents for simplified calculations. Examples include determining cargo contents, rose sales, and motorcycle proportions. Fraction-percent equivalence simplifies arithmetic and provides quick insights into ratios and totals. Applications include logistics, commerce, and urban planning.

Topic

Percents

Description

This video demonstrates how to handle multiple percentage changes applied sequentially, including discounts and price fluctuations. Examples include double-discounted items, stock price variations, and gasoline price changes. Applications emphasize consolidating multiple percents into single calculations for efficiency in financial and retail scenarios.

Topic

Percents

Description

This video covers calculating percent decreases in scenarios such as price reductions, vehicle depreciation, and cube dimension changes. Examples demonstrate the relationship between linear decreases and their exponential effects on surface area and volume. Applications include consumer goods, real estate, and geometry.

Topic

Percents

Description

The video explains how to calculate percent increases, focusing on changes in school enrollments, asset values, and cube dimensions. Examples highlight the non-linear effects of changes on surface area and volume. Applications include finance, education, and geometry, emphasizing understanding growth trends.

Topic

Percents

Description

The video discusses finding a percent difference when given a part that is not the focus of the percent. Scenarios include bus usage in schools, basketball free throws, and salmon spawning. It emphasizes adjusting percentages for complementary parts before solving equations. Applications highlight real-world uses in demographics, sports, and environmental studies.

Topic

Percents

Description

The video explains how to find the percent of a number by converting percents to fractions or decimals and performing multiplication. Examples include voter turnout in elections, body water composition, and ocean salt concentration. Key concepts include percent conversion and checking calculations using reverse operations. Applications include real-world scenarios such as population statistics and scientific measurements.

Topic

Percents

Description

The video explains the distinction between percent growth and multiple growth. Examples include doubling heights, stock price increases, and oil price changes. Applications emphasize clear understanding of percent versus multiplier concepts in finance and everyday math.

Topic

Percents

Description

The video explores percent-based probabilities in scenarios like dice rolls. Examples include calculating probabilities of specific outcomes and estimating occurrences over multiple trials. Applications include games of chance and statistical analysis.

Topic

Percents

Description

The video explains how to calculate simple interest using a formula involving principal, rate, and time. Examples include savings account growth, stock investments, and rare coin valuation. Applications include financial planning and historical item appraisal.

Topic

Percents

Description

This video focuses on calculating what percent one number is of another, using ratios and fractions. Examples include ratios in milk composition and inverses such as determining larger percents over 100. Applications show comparisons and understanding proportional relationships in varied contexts.

Topic

Percents

Description

Visual models such as grids and rectangles are used to represent percents and fractions for solving problems like transport usage, car distribution, and sales discounts. Examples include using grids to represent percentages of populations or products. Applications include educational tools and practical estimation.

Topic

Ratios

Description

Ratios are connected to percentages in this video. Examples include finding percentages of colored socks or non-green items in collections. It develops a formula for converting part-to-whole ratios into percentages.

Topic

Ratios

Description

The video covers practical applications of ratios for measuring slopes of roofs and ramps. Examples include comparing roof pitches, calculating base lengths of roofs, and determining ramp heights. Ratios provide clarity for gradual slopes.

Topic

Ratios

Description

The video covers practical applications of ratios for measuring slopes of roofs and ramps. Examples include comparing roof pitches, calculating base lengths of roofs, and determining ramp heights. Ratios provide clarity for gradual slopes.

Topic

Ratios

Description

This video illustrates converting ratios to percents using visual aids like area models and grids. Examples include determining percentages of colored eggs, fruit types, and combinations of colored lights.

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

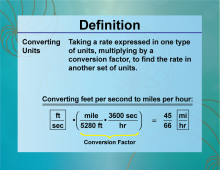
Topic

Ratios, Proportions, and Percents

Definition

Converting units involves changing a measurement from one unit to another using a conversion factor.

Description

Converting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters.

For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 

5 × 1.60934 = 8.0467 kilometers

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Equivalent ratios are ratios that express the same relationship between quantities.

Description

Equivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models.

For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-part ratios compare different parts of a whole to each other.

Description

Part-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics.

For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions.

Description

Part-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making.

Topic

Ratios, Proportions, and Percents

Definition

A percent is a ratio that compares a number to 100.

Description

Percentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates.

For example, if you score 45 out of 50 on a test, your percentage score is 

(45/50) × 100 = 90%

Topic

Ratios, Proportions, and Percents

Definition

Percent decrease measures the reduction in value expressed as a percentage of the original value.

Description

Percent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss.

For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as 

(80 − 60)/80 × 100 = 25%.

Topic

Ratios, Proportions, and Percents

Definition

Percent increase measures the growth in value expressed as a percentage of the original value.

Description

Percent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth.

For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as 

(75 − 50)/50 × 100 = 50%

Topic

Ratios, Proportions, and Percents

Definition

Percent of a number involves calculating the amount represented by a certain percentage of that number.

Description

Understanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping.

Topic

Ratios, Proportions, and Percents

Definition

Percent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity.

Description

Knowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount.

For instance, if 20% of an unknown number equals 15, you can set up the equation: 

0.20x = 15

Topic

Ratios, Proportions, and Percents

Definition

Percents as decimals involve converting a percentage into its decimal representation.

Description

Converting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100.

For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy.

Topic

Ratios, Proportions, and Percents

Definition

A proportion is an equation that states that two ratios are equal.

Description

Understanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models.

To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio.

Topic

Ratios, Proportions, and Percents

Definition

Proportional refers to the relationship between two quantities where their ratio is constant.

Description

Proportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering.

For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations.

Topic

Ratios, Proportions, and Percents

Definition

A rate is a ratio that compares two quantities with different units.

Description

Rates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting.

For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems.

Topic

Ratios, Proportions, and Percents

Definition

A ratio is a comparison of two quantities by division.

Description

Ratios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance.

For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations.

Topic

Ratios, Proportions, and Percents

Definition

Ratios and fractions are both ways of comparing quantities, with fractions representing a part of a whole.

Description

Understanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio.

Topic

Ratios, Proportions, and Percents

Definition

The slope of a line is a ratio that represents the change in y over the change in x.

Description

Understanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points.

For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields.