
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 10: The Distributive Property, Part 2
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Definitions Collection: Solving Equations | OverviewThe Equations collection on Media4Math is an invaluable resource for students and educators alike, offering a comprehensive set of definitions related to equations. This collection includes essential terms such as linear equations, quadratic equations, and polynomial equations. Each term is clearly defined, providing students with a solid foundation in understanding the various types of equations they will encounter in their studies. |
Numerical and Algebraic Expressions, Applications of Equations and Inequalities, Variable Expressions, Variables and Unknowns, Inequalities, Applications of Linear Functions, Solving Multistep Equations, Numerical Expressions, Solving One-Step Equations, Polynomial Functions and Equations, Quadratic Equations and Functions and Solving Two-Step Equations |

|
Math Definitions Collection: Variables and Unknowns |
OverviewThis collection aggregates all the definition image cards around the topic of Variables and Unknowns terms and vocabulary. There are a total of 20 terms. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.
|
Variables and Unknowns |

|
Math Video Definitions Collection: Equations | OverviewDiscover the comprehensive collection of videos on Equations Vocabulary. This curated series offers clear definitions and explanations of essential math terms related to equations, covering a wide range of concepts and skills. From foundational terms to more advanced vocabulary, these resources support students in mastering the language of math. |
Numerical and Algebraic Expressions, Applications of Equations and Inequalities, Variable Expressions, Variables and Unknowns, Inequalities, Applications of Linear Functions, Solving Multistep Equations, Numerical Expressions, Solving One-Step Equations, Polynomial Functions and Equations, Quadratic Equations and Functions and Solving Two-Step Equations |

|
Math Video Collection: Algebra Applications Video Series: Equations |
OverviewThis collection aggregates all the math videos and resources in this series: Algebra Applications Video Series: Equations. There are a total of 23 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
VIDEO: Algebra Applications: Variables and Equations | VIDEO: Algebra Applications: Variables and Equations
TopicEquations |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
VIDEO: Algebra Nspirations: Variables and Equations | VIDEO: Algebra Nspirations: Variables and Equations
TopicEquations |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Algebra Applications: Variables and Equations | Closed Captioned Video: Algebra Applications: Variables and EquationsTopicEquations |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Algebra Applications: Variables and Equations, 1 | Closed Captioned Video: Algebra Applications: Variables and Equations, 1TopicEquations DescriptionThe video introduces algebraic expressions and their ability to represent both known and unknown quantities. It defines variables as placeholders for unknowns and explains equations as relationships between two expressions. Key concepts include solving for variables and understanding the role of variables in equations. Key vocabulary includes variable, unknown quantity, and equation. The applications discussed include investigations into real-world scenarios such as honeybee populations and river geology. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Algebra Applications: Variables and Equations, 2 | Closed Captioned Video: Algebra Applications: Variables and Equations, 2TopicEquations DescriptionThe video investigates the geometry of river meanders using the concept of the meander ratio, calculated as the ratio of a river’s sinuous length to its straight-line length. It uses a TI-Nspire calculator to simulate river paths and compute ratios. Key vocabulary includes meander ratio, sinuous length, and geometric modeling. Applications highlight the mathematical modeling of natural phenomena and the occurrence of pi in nature. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Algebra Applications: Variables and Equations, 3 | Closed Captioned Video: Algebra Applications: Variables and Equations, 3TopicEquations DescriptionThis segment explores the impact of colony collapse disorder on honey production using statistical data. It introduces box and whisker plots and the calculation of mean as statistical tools to analyze honey yields. Key vocabulary includes colony collapse disorder, box plot, and mean. Applications include modeling bee population declines and their broader ecological and agricultural implications. |
Applications of Equations and Inequalities, Variables and Unknowns, Variable Expressions and Applications of Ratios, Proportions, and Percents |

|
Closed Captioned Video: Algebra Nspirations: Variables and Equations | Closed Captioned Video: Algebra Nspirations: Variables and Equations
Ever since the mathematics of the Babylonians, equations have played a central role in the development of algebra. Written and hosted by internationally acclaimed mathematics educator Dr. Monica Neagoy, this video traces the history and evolution of equations. It explores the two principal equations encountered in an introductory algebra course--linear and quadratic--in an engaging way. The foundations of algebra are explored and fundamental questions about the nature of algebra are answered. In addition, problems involving linear and quadratic equations are solved using the TI-Nspire graphing calculator. Algebra teachers looking to integrate hand-held technology and visual media into their instruction will benefit greatly from this series. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Algebra Nspirations: Variables and Equations, 1 | Closed Captioned Video: Algebra Nspirations: Variables and Equations, Segment 1
In this Investigation we get a historical overview of equations. This video is Segment 1 of a 2 segment series related to Variables and Equations. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Algebra Nspirations: Variables and Equations, 3 | Closed Captioned Video: Algebra Nspirations: Variables and Equations, Segment 3
In this Investigation we solve linear and quadratic equations. This video is Segment 3 of a 4 segment series related to Variables and Equations. Segments 3 and 4 are grouped together. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: Overview of Variables and Equations | Closed Captioned Video: Overview of Variables and Equations
In this video segment, get an overview of variables and equations, along with the evolution of algebraic notation. |
Applications of Equations and Inequalities, Variables and Unknowns and Variable Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b negative
Video Tutorial: The Distributive Property: a(-x + b), a negative, b negative. In this video use the distributive property with an expression of the form a(-x + b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(-x + b), a negative, b positive
Video Tutorial: The Distributive Property: a(-x + b), a negative, b positive. In this video use the distributive property with an expression of the form a(-x + b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x + b), all constants positive | Closed Captioned Video: The Distributive Property: a(-x + b), all constants positive
Video Tutorial: The Distributive Property: a(-x + b), all constants positive. In this video use the distributive property with an expression of the form a(-x + b), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b negative
Video Tutorial: The Distributive Property: a(-x - b), a negative, b negative. In this video use the distributive property with an expression of the form a(-x - b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(-x - b), a negative, b positive
Video Tutorial: The Distributive Property: a(-x - b), a negative, b positive. In this video, we will use the distributive property with an expression of the form a(-x - b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(-x - b), all constants positive | Closed Captioned Video: The Distributive Property: a(-x - b), all constants positive
Video Tutorial: The Distributive Property: a(-x - b), all constants positive. In this video use the distributive property with an expression of the form a(-x - b), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx + c), a negative, b and c positive | Closed Captioned Video: The Distributive Property: a(bx + c), a negative, b and c positive
Video Tutorial: The Distributive Property: a(bx + c), a negative, b and c positive. In this video, we will use the distributive property with an expression of the form a(bx + c), a negative, b and c positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx + c), all constants negative | Closed Captioned Video: The Distributive Property: a(bx + c), all constants negative
Video Tutorial: The Distributive Property: a(bx + c), all constants negative. In this video use the distributive property with an expression of the form a(bx + c), all negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx + c), all constants positive | Closed Captioned Video: The Distributive Property: a(bx + c), all constants positive
Video Tutorial: The Distributive Property: a(bx + c), all constants positive. In this video use the distributive property with an expression of the form a(bx + c), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx - c), a negative, b and c positive | Closed Captioned Video: The Distributive Property: a(bx - c), a negative, b and c positive
Video Tutorial: The Distributive Property: a(bx - c), a negative, b and c positive. In this video use the distributive property with an expression of the form a(bx - c), a negative, b and c positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx - c), all constants negative | Closed Captioned Video: The Distributive Property: a(bx - c), all constants negative
Video Tutorial: The Distributive Property: a(bx - c), all constants negative. In this video, we will use the distributive property with an expression of the form a(bx - c), all negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(bx - c), all constants positive | Closed Captioned Video: The Distributive Property: a(bx - c), all constants positive
Video Tutorial: The Distributive Property: a(bx - c), all constants positive. In this video use the distributive property with an expression of the form a(bx - c), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(x + b), a negative, b negative
Video Tutorial: The Distributive Property: a(x + b), a negative, b negative. In this video use the distributive property with an expression of the form a(x + b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x + b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(x + b), a negative, b positive
Video Tutorial: The Distributive Property: a(x + b), a negative, b positive. In this video, we will use the distributive property with an expression of the form a(x + b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x + b), all constants positive | Closed Captioned Video: The Distributive Property: a(x + b), all constants positive
Video Tutorial: The Distributive Property: a(x + b), all constants positive. In this video, we will use the distributive property with an expression of the form a(x + b), all constants positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b negative | Closed Captioned Video: The Distributive Property: a(x - b), a negative, b negative
Video Tutorial: The Distributive Property: a(x - b), a negative, b negative. In this video, we will use the distributive property with an expression of the form a(x - b), a negative, b negative. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x - b), a negative, b positive | Closed Captioned Video: The Distributive Property: a(x - b), a negative, b positive
Video Tutorial: The Distributive Property: a(x - b), a negative, b positive. In this video use the distributive property with an expression of the form a(x - b), a negative, b positive. |
Numerical and Algebraic Expressions |

|
Closed Captioned Video: The Distributive Property: a(x - b), all constants positive | Closed Captioned Video: The Distributive Property: a(x - b), all constants positive
Video Tutorial: The Distributive Property: a(x - b), all constants positive. In this video, we will use the distributive property with an expression of the form a(x - b), all constants positive. |
Numerical and Algebraic Expressions |

|
Definition--Equation Concepts--Constant Term | Constant TermTopicEquations DefinitionA constant term is a term in an algebraic expression that does not contain any variables. DescriptionConstant terms are fixed values in algebraic expressions and equations. They do not change because they lack variables. For example, in the expression 3x + 4 the number 4 is a constant term. Constant terms are essential in forming and solving equations. |
Variables and Unknowns |

|
Definition--Equation Concepts--Isolating the Variable | Isolating the VariableTopicEquations DefinitionIsolating the variable involves manipulating an equation to get the variable alone on one side. DescriptionIsolating the variable is a fundamental technique in algebra used to solve equations. It involves performing operations to both sides of an equation to get the variable by itself. For example, solving 2x + 3 = 7 involves subtracting 3 and then dividing by 2 to isolate x, resulting in x = 2. |
Variables and Unknowns |

|
Definition--Equation Concepts--The Unknown | The UnknownTopicEquations DefinitionThe unknown is the variable in an equation that needs to be solved for. DescriptionThe unknown in an equation represents the value that needs to be determined. For example, in the equation x + 3 = 7 x is the unknown. Identifying and solving for the unknown is a core aspect of algebra. In real-world applications, finding the unknown is crucial for solving problems in various fields such as science, engineering, and finance. Understanding how to identify and solve for the unknown helps students develop problem-solving skills and apply mathematical concepts to real-life situations. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Algebraic Expression | Definition--Variables, Unknowns, and Constants--Algebraic Expression
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Assigning Values to Variables | Definition--Variables, Unknowns, and Constants--Assigning Values to Variables
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Coefficient | What Is a Coefficient?
This is part of a series of definitions that focus on constants, variables, and coefficients. These definition cards can easily be incorporated into a lesson plan. —PRESS PREVIEW TO SEE THE DEFINITION— To see the complete collection of definitions on this topic, click on this link.The following section provides a brief review of number properties that are helpful in working with numerical and variable expressions. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Constant | Definition--Variables, Unknowns, and Constants--Constant
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Constant of Proportionality | Definition--Variables, Unknowns, and Constants--Constant of Proportionality
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Constant of Variation | Definition--Variables, Unknowns, and Constants--Constant of Variation
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Constant Term | Definition--Variables, Unknowns, and Constants--Constant Term
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Evaluating an Algebraic Expression | Definition--Variables, Unknowns, and Constants--Evaluating an Algebraic Expression
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |
|
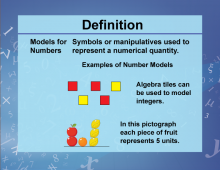
Definition--Variables, Unknowns, and Constants--Models for Numbers | Definition--Variables, Unknowns, and Constants--Models for Numbers
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Models for Variables | Definition--Variables, Unknowns, and Constants--Models for Variables
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Numerical Expression | Definition--Variables, Unknowns, and Constants--Numerical Expression
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |
|
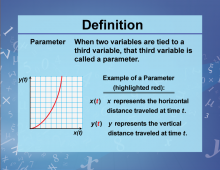
Definition--Variables, Unknowns, and Constants--Parameter | Definition--Variables, Unknowns, and Constants--Parameter
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Random Variable | Definition--Variables, Unknowns, and Constants--Random Variable
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Range of a Variable | Definition--Variables, Unknowns, and Constants--Range of a Variable
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |

|
Definition--Variables, Unknowns, and Constants--Solving for the Unknown | Definition--Variables, Unknowns, and Constants--Solving for the Unknown
This is part of a collection of definitions related to variables, unknowns, and constants. This includes general definitions for variables, unknowns, and constants, as well as related terms that describe their properties. |
Variables and Unknowns |