
Illustrative Math Alignment: Grade 6 Unit 7
Rational Numbers
Lesson 19: Drawing on the Coordinate Plane
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Math Examples Collection: The Distance Formula | OverviewThis collection aggregates all the math examples around the topic of the Distance Formula. There are a total of 21 Math Examples. This collection of resources is made up of downloadable JPG images that you can easily incorporate into your lesson plans. |
The Distance Formula |

|
Math Worksheet Collection: The Distance Formula |
OverviewThis collection aggregates all the math worksheets around the topic of the Distance Formula. There are a total of 160 worksheets. Each worksheet includes an answer key. This collection of resources is made up of downloadable PDF files that you can easily incorporate into your instruction.To download the full set of these resources, click on this link.
|
Distance Formula and The Distance Formula |

|
Math Worksheet Collection: Using Distance Formula for Area and Perimeter |
OverviewThis collection aggregates all the math worksheets around the topic of Using Distance Formula for Area and Perimeter. There are a total of 140 worksheets. Each worksheet includes an answer key. This collection of resources is made up of downloadable PDF files that you can easily incorporate into your instruction.
|
Distance Formula and The Distance Formula |

|
Math Quiz Collection: The Distance Formula |
OverviewThis collection aggregates all the math quizzes on this topic: The Distance Formula. There are a total of 3 resources. This collection of quizzes is made up of downloadable PDFs. To download the full set of these resources, click on this link.
|
Distance Formula and The Distance Formula |

|
Math Definitions Collection: Geometry | OverviewThe Geometry Basics collection from Media4Math is an essential resource for educators looking to enhance their students' understanding of fundamental geometric concepts. This comprehensive set includes 58 terms, each presented as a downloadable PNG image card that can be seamlessly integrated into classroom presentations. |
Definition of an Angle, Geometric Constructions with Points and Lines, 3-Dimensional Figures, Exploring Coordinate Systems, Definition of a Triangle, Definition of a Point, Definition of a Circle, Definition of Transformations, The Distance Formula, Definition of a Polygon, Definition of a Plane, Definition of a Line, Midpoint Formula, Applications of Polygons, Area and Perimeter of Triangles, Area and Perimeter of Quadrilaterals, Pyramids, Trig Expressions and Identities, Right Triangles, Definition of a Quadrilateral, Applications of Points and Lines and Proportions |

|
Lesson Plan Collection: SAT Math | SAT Math Prep Course | 35-Lesson Unit Prepare for the SAT Math Test with this comprehensive and growing collection of expertly designed SAT Math lesson plans from Media4Math. Whether you're a teacher, tutor, or student, these lessons offer clear, structured, and standards-aligned instruction across the full range of SAT Math topics. |
Slope-Intercept Form, Solving Two-Step Equations, Inequalities, Solving Systems of Equations, Applications of Linear Functions, Special Functions, Applications of Linear Systems, Applications of Ratios, Proportions, and Percents, Percents, Ratios and Rates, Variable Expressions, Data Analysis, Probability, Quadratic Equations and Functions, Quadratic Formula, Exponential and Logarithmic Functions and Equations, Rational Functions and Equations, Relations and Functions, Functions and Their Inverses, Polynomial Functions and Equations, Applications of Quadratic Functions, Applications of Exponential and Logarithmic Functions, Parallel Lines, Applications of Triangles, Applications of Circles, Geometric Constructions with Circles, Applications of Quadrilaterals, Definition of a Quadrilateral, Applications of Coordinate Geometry, The Distance Formula, Applications of Transformations, Trig Expressions and Identities, Trigonometric Functions and Complex Numbers |

|
Definition--Geometry Basics--Distance Formula | Distance FormulaTopicGeometry Basics DefinitionThe distance formula is used to determine the distance between two points in a coordinate plane. DescriptionThe distance formula is derived from the Pythagorean Theorem and is given by |
The Distance Formula |

|
INSTRUCTIONAL RESOURCE: Math Examples 9 | INSTRUCTIONAL RESOURCE: Math Examples--Distance Formula
The complete set of 21 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Distance Formula and The Distance Formula |
|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Coordinate Grid | Math Clip Art--Coordinate Geometry--Coordinate GridTopicGeometry Concepts DescriptionThis image depicts a coordinate grid, a fundamental tool in coordinate geometry used to plot points, lines, and shapes. The grid consists of horizontal and vertical lines that intersect at right angles, creating a series of squares. Coordinate grids are essential for understanding the Cartesian coordinate system, where each point is defined by an ordered pair of numbers (x, y). This system is used in various fields, including mathematics, physics, engineering, and computer graphics, to represent and analyze spatial relationships. |
Exploring Coordinate Systems and Coordinate Systems |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Coordinate Grid | Math Clip Art--Coordinate Geometry--Coordinate GridTopicGeometry Concepts DescriptionThis image depicts a coordinate grid, a fundamental tool in coordinate geometry used to plot points, lines, and shapes. The grid consists of horizontal and vertical lines that intersect at right angles, creating a series of squares. Coordinate grids are essential for understanding the Cartesian coordinate system, where each point is defined by an ordered pair of numbers (x, y). This system is used in various fields, including mathematics, physics, engineering, and computer graphics, to represent and analyze spatial relationships. |
Exploring Coordinate Systems and Coordinate Systems |
|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Coordinate Grid--Blank | Math Clip Art--Coordinate Geometry--Coordinate Grid--BlankTopicGeometry Concepts DescriptionThis image shows a blank coordinate grid, which serves as a versatile tool for plotting points, lines, and shapes in coordinate geometry. The grid provides a structured framework for visualizing mathematical concepts and relationships. Blank coordinate grids are commonly used in educational settings to teach students about graphing, transformations, and spatial reasoning. They allow for hands-on exploration of mathematical ideas and are essential for developing a deep understanding of the Cartesian coordinate system. |
Exploring Coordinate Systems and Coordinate Systems |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Coordinate Grid--Blank | Math Clip Art--Coordinate Geometry--Coordinate Grid--BlankTopicGeometry Concepts DescriptionThis image shows a blank coordinate grid, which serves as a versatile tool for plotting points, lines, and shapes in coordinate geometry. The grid provides a structured framework for visualizing mathematical concepts and relationships. Blank coordinate grids are commonly used in educational settings to teach students about graphing, transformations, and spatial reasoning. They allow for hands-on exploration of mathematical ideas and are essential for developing a deep understanding of the Cartesian coordinate system. |
Exploring Coordinate Systems and Coordinate Systems |
|
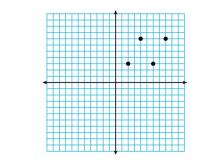
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q1 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q1TopicGeometry Concepts DescriptionThis image illustrates points plotted on a coordinate grid in the first quadrant (Q1). In Q1, both x and y coordinates are positive, making it a key area for graphing and analyzing functions. Connecting these points would result in a parallelogram. Understanding how to plot points in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing linear equations, analyzing functions, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q1 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q1TopicGeometry Concepts DescriptionThis image illustrates points plotted on a coordinate grid in the first quadrant (Q1). In Q1, both x and y coordinates are positive, making it a key area for graphing and analyzing functions. Connecting these points would result in a parallelogram. Understanding how to plot points in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing linear equations, analyzing functions, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q1 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q1TopicGeometry Concepts DescriptionThis image illustrates points plotted on a coordinate grid in the first quadrant (Q1). In Q1, both x and y coordinates are positive, making it a key area for graphing and analyzing functions. Connecting these points would result in a parallelogram. Understanding how to plot points in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing linear equations, analyzing functions, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |
|
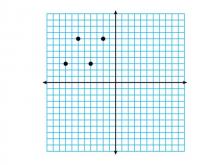
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q2 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q2TopicGeometry Concepts DescriptionThis image shows points plotted on a coordinate grid in the second quadrant (Q2). In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Connecting these points would result in a parallelogram. Plotting points in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q2 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q2TopicGeometry Concepts DescriptionThis image shows points plotted on a coordinate grid in the second quadrant (Q2). In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Connecting these points would result in a parallelogram. Plotting points in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q2 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q2TopicGeometry Concepts DescriptionThis image shows points plotted on a coordinate grid in the second quadrant (Q2). In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Connecting these points would result in a parallelogram. Plotting points in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |
|
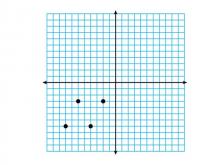
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q3 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q3TopicGeometry Concepts DescriptionThis image depicts points plotted on a coordinate grid in the third quadrant (Q3). In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Connecting these points would result in a parallelogram. Plotting points in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q3 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q3TopicGeometry Concepts DescriptionThis image depicts points plotted on a coordinate grid in the third quadrant (Q3). In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Connecting these points would result in a parallelogram. Plotting points in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q3 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q3TopicGeometry Concepts DescriptionThis image depicts points plotted on a coordinate grid in the third quadrant (Q3). In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Connecting these points would result in a parallelogram. Plotting points in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |
|
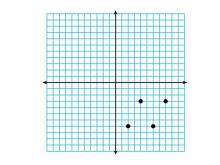
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q4 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q4TopicGeometry Concepts DescriptionThis image illustrates points plotted on a coordinate grid in the fourth quadrant (Q4). In Q4, the x-coordinates are positive while the y-coordinates are negative, completing the understanding of the Cartesian plane. Connecting these points would result in a parallelogram. Understanding how to plot points in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q4 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q4TopicGeometry Concepts DescriptionThis image illustrates points plotted on a coordinate grid in the fourth quadrant (Q4). In Q4, the x-coordinates are positive while the y-coordinates are negative, completing the understanding of the Cartesian plane. Connecting these points would result in a parallelogram. Understanding how to plot points in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Points on Coordinate Grid--Q4 | Math Clip Art--Coordinate Geometry--Points on Coordinate Grid--Q4TopicGeometry Concepts DescriptionThis image illustrates points plotted on a coordinate grid in the fourth quadrant (Q4). In Q4, the x-coordinates are positive while the y-coordinates are negative, completing the understanding of the Cartesian plane. Connecting these points would result in a parallelogram. Understanding how to plot points in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines |
|
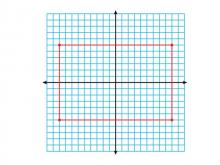
Math Clip Art--Geometry Concepts--Coordinate Geometry--Rectangle Centered at the Origin | Math Clip Art--Coordinate Geometry--Rectangle Centered at the OriginTopicGeometry Concepts DescriptionThis image illustrates a rectangle centered at the origin of a coordinate grid. The rectangle's position allows for easy analysis of its properties, such as symmetry and dimensions, using the Cartesian coordinate system. Understanding how to position geometric shapes at the origin is crucial for exploring concepts like symmetry, transformations, and coordinate geometry. This setup simplifies calculations involving distance, midpoint, and area. |
Definition of a Quadrilateral |
|
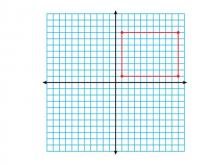
Math Clip Art--Geometry Concepts--Coordinate Geometry--Rectangle in Q1 | Math Clip Art--Coordinate Geometry--Rectangle in Q1TopicGeometry Concepts DescriptionThis image depicts a rectangle positioned in the first quadrant (Q1) of a coordinate grid. In Q1, both the x and y coordinates are positive, making it a straightforward area for graphing and analysis. Placing a rectangle in Q1 helps students understand the relationship between geometric shapes and their coordinate representations. It is useful for exploring concepts like area, perimeter, and transformations. |
Definition of a Quadrilateral |
|
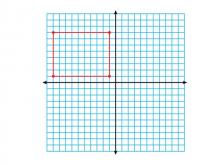
Math Clip Art--Geometry Concepts--Coordinate Geometry--Rectangle in Q2 | Math Clip Art--Coordinate Geometry--Rectangle in Q2TopicGeometry Concepts DescriptionThis image shows a rectangle positioned in the second quadrant (Q2) of a coordinate grid. In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Understanding how to place rectangles in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Definition of a Quadrilateral |
|
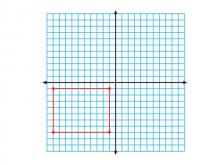
Math Clip Art--Geometry Concepts--Coordinate Geometry--Rectangle in Q3 | Math Clip Art--Coordinate Geometry--Rectangle in Q3TopicGeometry Concepts DescriptionThis image illustrates a rectangle positioned in the third quadrant (Q3) of a coordinate grid. In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Placing rectangles in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Definition of a Quadrilateral |
|
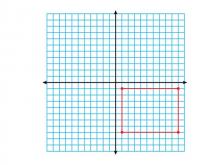
Math Clip Art--Geometry Concepts--Coordinate Geometry--Rectangle in Q4 | Math Clip Art--Coordinate Geometry--Rectangle in Q4TopicGeometry Concepts DescriptionThis image depicts a rectangle positioned in the fourth quadrant (Q4) of a coordinate grid. In Q4, the x-coordinates are positive while the y-coordinates are negative, completing the understanding of the Cartesian plane. Understanding how to place rectangles in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing functions, analyzing data, and exploring geometric transformations. |
Definition of a Quadrilateral |
|
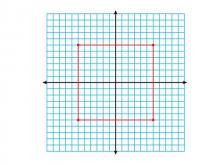
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square Centered at the Origin | Math Clip Art--Coordinate Geometry--Square Centered at the OriginTopicGeometry Concepts DescriptionThis image illustrates a square centered at the origin of a coordinate grid. The square's position allows for easy analysis of its properties, such as symmetry and dimensions, using the Cartesian coordinate system. Understanding how to position geometric shapes at the origin is crucial for exploring concepts like symmetry, transformations, and coordinate geometry. This setup simplifies calculations involving distance, midpoint, and area. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square Centered at the Origin | Math Clip Art--Coordinate Geometry--Square Centered at the OriginTopicGeometry Concepts DescriptionThis image illustrates a square centered at the origin of a coordinate grid. The square's position allows for easy analysis of its properties, such as symmetry and dimensions, using the Cartesian coordinate system. Understanding how to position geometric shapes at the origin is crucial for exploring concepts like symmetry, transformations, and coordinate geometry. This setup simplifies calculations involving distance, midpoint, and area. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |
|
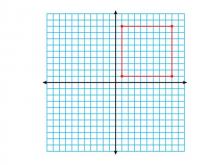
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q1 | Math Clip Art--Coordinate Geometry--Square in Q1TopicGeometry Concepts DescriptionThis image depicts a square positioned in the first quadrant (Q1) of a coordinate grid. In Q1, both the x and y coordinates are positive, making it a straightforward area for graphing and analysis. Placing a square in Q1 helps students understand the relationship between geometric shapes and their coordinate representations. It is useful for exploring concepts like area, perimeter, and transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q1 | Math Clip Art--Coordinate Geometry--Square in Q1TopicGeometry Concepts DescriptionThis image depicts a square positioned in the first quadrant (Q1) of a coordinate grid. In Q1, both the x and y coordinates are positive, making it a straightforward area for graphing and analysis. Placing a square in Q1 helps students understand the relationship between geometric shapes and their coordinate representations. It is useful for exploring concepts like area, perimeter, and transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |
|
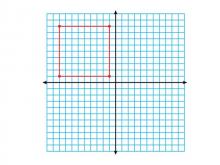
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q2 | Math Clip Art--Coordinate Geometry--Square in Q2TopicGeometry Concepts DescriptionThis image shows a square positioned in the second quadrant (Q2) of a coordinate grid. In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Understanding how to place squares in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q2 | Math Clip Art--Coordinate Geometry--Square in Q2TopicGeometry Concepts DescriptionThis image shows a square positioned in the second quadrant (Q2) of a coordinate grid. In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Understanding how to place squares in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |
|
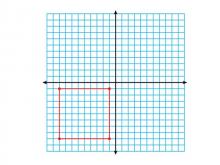
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q3 | Math Clip Art--Coordinate Geometry--Square in Q3TopicGeometry Concepts DescriptionThis image illustrates a square positioned in the third quadrant (Q3) of a coordinate grid. In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Placing squares in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q3 | Math Clip Art--Coordinate Geometry--Square in Q3TopicGeometry Concepts DescriptionThis image illustrates a square positioned in the third quadrant (Q3) of a coordinate grid. In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Placing squares in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |
|
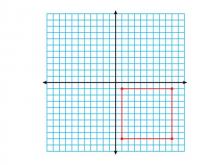
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q4 | Math Clip Art--Coordinate Geometry--Square in Q4TopicGeometry Concepts DescriptionThis image depicts a square positioned in the fourth quadrant (Q4) of a coordinate grid. In Q4, the x-coordinates are positive while the y-coordinates are negative, completing the understanding of the Cartesian plane. Understanding how to place squares in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Square in Q4 | Math Clip Art--Coordinate Geometry--Square in Q4TopicGeometry Concepts DescriptionThis image depicts a square positioned in the fourth quadrant (Q4) of a coordinate grid. In Q4, the x-coordinates are positive while the y-coordinates are negative, completing the understanding of the Cartesian plane. Understanding how to place squares in different quadrants is fundamental in coordinate geometry. It helps students develop skills in graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Definition of a Quadrilateral |
|
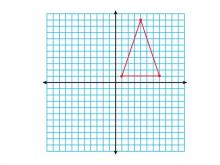
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q1 | Math Clip Art--Coordinate Geometry--Triangle in Q1TopicGeometry Concepts DescriptionThis image illustrates a triangle positioned in the first quadrant (Q1) of a coordinate grid. In Q1, both the x and y coordinates are positive, making it a straightforward area for graphing and analysis. Placing a triangle in Q1 helps students understand the relationship between geometric shapes and their coordinate representations. It is useful for exploring concepts like area, perimeter, and transformations. |
Applications of Coordinate Geometry and Applications of Triangles |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q1 | Math Clip Art--Coordinate Geometry--Triangle in Q1TopicGeometry Concepts DescriptionThis image illustrates a triangle positioned in the first quadrant (Q1) of a coordinate grid. In Q1, both the x and y coordinates are positive, making it a straightforward area for graphing and analysis. Placing a triangle in Q1 helps students understand the relationship between geometric shapes and their coordinate representations. It is useful for exploring concepts like area, perimeter, and transformations. |
Applications of Coordinate Geometry and Applications of Triangles |
|
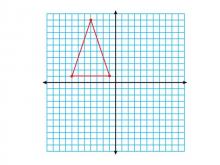
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q2 | Math Clip Art--Coordinate Geometry--Triangle in Q2TopicGeometry Concepts DescriptionThis image shows a triangle positioned in the second quadrant (Q2) of a coordinate grid. In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Understanding how to place triangles in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry and Applications of Triangles |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q2 | Math Clip Art--Coordinate Geometry--Triangle in Q2TopicGeometry Concepts DescriptionThis image shows a triangle positioned in the second quadrant (Q2) of a coordinate grid. In Q2, the x-coordinates are negative while the y-coordinates are positive, which is important for understanding the full Cartesian plane. Understanding how to place triangles in different quadrants helps students grasp the concept of negative and positive values in coordinate geometry. It is crucial for graphing functions, analyzing data, and understanding geometric transformations. |
Applications of Coordinate Geometry and Applications of Triangles |
|
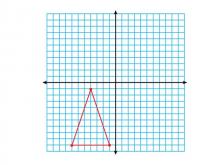
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q3 | Math Clip Art--Coordinate Geometry--Triangle in Q3TopicGeometry Concepts DescriptionThis image illustrates a triangle positioned in the third quadrant (Q3) of a coordinate grid. In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Placing triangles in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Applications of Triangles |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q3 | Math Clip Art--Coordinate Geometry--Triangle in Q3TopicGeometry Concepts DescriptionThis image illustrates a triangle positioned in the third quadrant (Q3) of a coordinate grid. In Q3, both x and y coordinates are negative, which is essential for understanding the complete Cartesian coordinate system. Placing triangles in different quadrants helps students understand the concept of negative values and their implications in geometry. It is crucial for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Applications of Triangles |
|
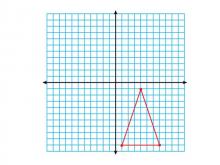
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q4 | Math Clip Art--Coordinate Geometry--Triangle in Q4TopicGeometry Concepts DescriptionThis image depicts a triangle positioned in the fourth quadrant (Q4) of a coordinate grid. In Q4, the x-coordinates are positive while the y-coordinates are negative, which is crucial for understanding the complete Cartesian plane. Placing a triangle in Q4 helps students understand the implications of positive and negative values in coordinate geometry. This understanding is essential for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Applications of Triangles |

|
Math Clip Art--Geometry Concepts--Coordinate Geometry--Triangle in Q4 | Math Clip Art--Coordinate Geometry--Triangle in Q4TopicGeometry Concepts DescriptionThis image depicts a triangle positioned in the fourth quadrant (Q4) of a coordinate grid. In Q4, the x-coordinates are positive while the y-coordinates are negative, which is crucial for understanding the complete Cartesian plane. Placing a triangle in Q4 helps students understand the implications of positive and negative values in coordinate geometry. This understanding is essential for graphing functions, analyzing data, and exploring geometric transformations. |
Applications of Coordinate Geometry and Applications of Triangles |
|
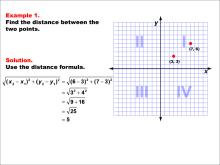
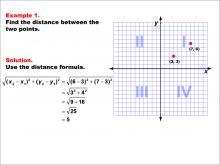
Math Example--Coordinate Geometry--Distance Formula: Example 1 | Math Example--Coordinate Geometry--Distance Formula: Example 1TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (3, 3) and (7, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - 3)2 + (7 - 3)2) = 5. |
The Distance Formula |
|
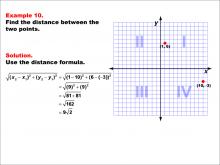
Math Example--Coordinate Geometry--Distance Formula: Example 10 | Math Example--Coordinate Geometry--Distance Formula: Example 10TopicGeometry DescriptionThis example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (1, 6) and (10, -3) are plotted on a graph, and the distance between them is determined using the formula: √((1 - 10)2 + (6 - (-3))2) = √(9^2 + 9^2) = √162 = 9√2. |
The Distance Formula |
|
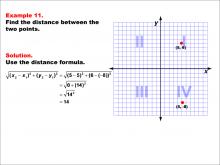
Math Example--Coordinate Geometry--Distance Formula: Example 11 | Math Example--Coordinate Geometry--Distance Formula: Example 11TopicGeometry DescriptionThis example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (5, 6) and (5, -8) are plotted on a graph, and the distance between them is calculated using the formula: √((5 - 5)2 + (6 - (-8))2) = √(0 + (14)2) = 14. |
The Distance Formula |