Illustrative Math Alignment: Grade 7 Unit 2

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Why do rivers meander instead of traveling in a straight line? In going from point A to point B, why should a river take the circuitous route it does instead of a direct path? Furthermore, what information can the ratio of the river’s length to its straight-line distance tell us? In this segment the geological forces that account for a river’s motion are explained. In the process, the so-called Meander Ratio is explored. Students construct a mathematical model of a meandering river using the TI-Nspire. Having built the model, students then use it to generate data to find the average of many Meander Ratios. The results show that on average the Meander Ratio is equal to pi.

Video Tutorial: Ratios and Proportions: Scale Drawings. In this video, we look at the properties of similar figures and use proportions to find lengths of corresponding sides.

Video Tutorial: Ratios and Proportions: Solving Proportions. In this video, we solve proportion problems algebraically.

Video Tutorial: Ratios and Proportions: What are Proportions?. In this video, we solve proportion problems using equivalent ratios.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items. Let's look at an example.

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

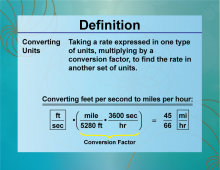
Topic

Ratios, Proportions, and Percents

Definition

Converting units involves changing a measurement from one unit to another using a conversion factor.

Description

Converting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters.

For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 

5 × 1.60934 = 8.0467 kilometers

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Equivalent ratios are ratios that express the same relationship between quantities.

Description

Equivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models.

For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-part ratios compare different parts of a whole to each other.

Description

Part-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics.

For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions.

Description

Part-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making.

Topic

Ratios, Proportions, and Percents

Definition

A percent is a ratio that compares a number to 100.

Description

Percentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates.

For example, if you score 45 out of 50 on a test, your percentage score is 

(45/50) × 100 = 90%

Topic

Ratios, Proportions, and Percents

Definition

Percent decrease measures the reduction in value expressed as a percentage of the original value.

Description

Percent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss.

For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as 

(80 − 60)/80 × 100 = 25%.

Topic

Ratios, Proportions, and Percents

Definition

Percent increase measures the growth in value expressed as a percentage of the original value.

Description

Percent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth.

For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as 

(75 − 50)/50 × 100 = 50%

Topic

Ratios, Proportions, and Percents

Definition

Percent of a number involves calculating the amount represented by a certain percentage of that number.

Description

Understanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping.

Topic

Ratios, Proportions, and Percents

Definition

Percent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity.

Description

Knowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount.

For instance, if 20% of an unknown number equals 15, you can set up the equation: 

0.20x = 15

Topic

Ratios, Proportions, and Percents

Definition

Percents as decimals involve converting a percentage into its decimal representation.

Description

Converting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100.

For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy.

Topic

Ratios, Proportions, and Percents

Definition

A proportion is an equation that states that two ratios are equal.

Description

Understanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models.

To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio.

Topic

Ratios, Proportions, and Percents

Definition

Proportional refers to the relationship between two quantities where their ratio is constant.

Description

Proportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering.

For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations.