
Illustrative Math Alignment: Grade 8 Unit 2
Dilations, Similarity, and Introducing Slope
Lesson 3: Dilations with no Grid
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
Math Clip Art Collection: Triangles |
OverviewThis collection aggregates all the math clip art around the topic of Triangles. There are a total of 14 images. This collection of resources is made up of downloadable PNG files that you can easily incorporate into a presentation.To download the full set of these resources, click on this link.
|
Applications of Coordinate Geometry, Applications of Triangles, Definition of a Triangle and Right Triangles |
|
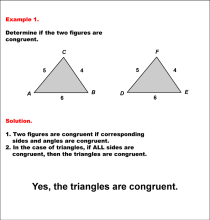
Math Examples Collection: Analyzing Congruent Shapes | OverviewThe Media4Math collection on Analyzing Congruent Shapes provides a comprehensive set of math examples designed to deepen students' understanding of congruence. These examples cover a range of skills, starting with basic shape identification and progressing to more complex applications of congruence in transformations and geometric reasoning. By presenting examples that increase in complexity, students are guided step-by-step to master the concept of congruence in a structured way. |
Definition of a Triangle |

|
INSTRUCTIONAL RESOURCE: Activity Guide: Building a Scale Model of Himeji Castle | This hands-on activity is a companion to the video segment from the Geometry Applications: Angles and Planes video. In particular, it supports the segment on the architecture of Himeji Castle. Note: The download is a PDF file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Applications of Angles and Planes, Applications of Transformations and Proportions |
|
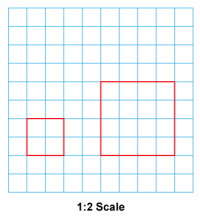
Math Clip Art--Geometry Concepts--Scale Drawing--01 | Math Clip Art--Scale Drawing--01TopicGeometry Concepts DescriptionThis image depicts a scale drawing of a square that has been scaled up by a factor of 1:2. This means that each side of the square in the drawing is twice the length of the corresponding side in the actual object. Scale drawings are essential for accurately representing objects in a manageable size while maintaining proportionality. Teacher's Script: "Observe this scale drawing of a square. How does the 1:2 scale factor help us understand the relationship between the drawing and the actual square? What are some real-world applications of scaling up objects, such as in architecture or design?" |
Proportions |

|
Math Clip Art--Geometry Concepts--Scale Drawing--02 | Math Clip Art--Scale Drawing--02TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a square that has been scaled up by a factor of 1:3. Each side of the square in the drawing is three times the length of the corresponding side in the actual object. This scaling helps in visualizing larger versions of objects while maintaining accurate proportions. Teacher's Script: "Look at this scale drawing of a square. How does the 1:3 scale factor affect the dimensions of the drawing compared to the actual square? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
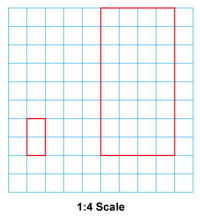
Math Clip Art--Geometry Concepts--Scale Drawing--03 | Math Clip Art--Scale Drawing--03TopicGeometry Concepts DescriptionThis image shows a scale drawing of a rectangle that has been scaled up by a factor of 1:4. Each side of the rectangle in the drawing is four times the length of the corresponding side in the actual object. This scaling is useful for enlarging objects while maintaining their proportional dimensions. Teacher's Script: "Examine this scale drawing of a rectangle. How does the 1:4 scale factor influence the size of the drawing compared to the actual rectangle? What are some real-world applications of scaling up objects, such as in engineering or construction?" |
Proportions |

|
Math Clip Art--Geometry Concepts--Scale Drawing--04 | Math Clip Art--Scale Drawing--04TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a rectangle that has been scaled up by a factor of 1:5. Each side of the rectangle in the drawing is five times the length of the corresponding side in the actual object. Scale drawings like this are crucial for visualizing larger versions of objects while maintaining accurate proportions. Teacher's Script: "Observe this scale drawing of a rectangle. How does the 1:5 scale factor affect the dimensions of the drawing compared to the actual rectangle? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
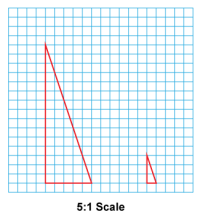
Math Clip Art--Geometry Concepts--Scale Drawing--05 | Math Clip Art--Scale Drawing--05TopicGeometry Concepts DescriptionThis image depicts a scale drawing of a right triangle that has been scaled down by a factor of 5:1. This means each side of the triangle in the drawing is one-fifth the length of the corresponding side in the actual object. Scaling down is useful for creating manageable representations of larger objects. Teacher's Script: "Examine this scale drawing of a right triangle. How does the 5:1 scale factor help us understand the relationship between the drawing and the actual triangle? What are some real-world applications of scaling down objects, such as in model making or map creation?" |
Proportions |
|
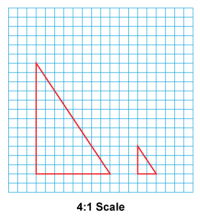
Math Clip Art--Geometry Concepts--Scale Drawing--06 | Math Clip Art--Scale Drawing--06TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a right triangle that has been scaled down by a factor of 4:1. Each side of the triangle in the drawing is one-fourth the length of the corresponding side in the actual object. This scaling helps in visualizing smaller versions of objects while maintaining accurate proportions. Teacher's Script: "Observe this scale drawing of a right triangle. How does the 4:1 scale factor affect the dimensions of the drawing compared to the actual triangle? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
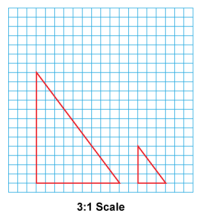
Math Clip Art--Geometry Concepts--Scale Drawing--07 | Math Clip Art--Scale Drawing--07TopicGeometry Concepts DescriptionThis image depicts a scale drawing of a right triangle that has been scaled down by a factor of 3:1. Each side of the triangle in the drawing is one-third the length of the corresponding side in the actual object. Scaling down is useful for creating manageable representations of larger objects. Teacher's Script: "Examine this scale drawing of a right triangle. How does the 3:1 scale factor help us understand the relationship between the drawing and the actual triangle? What are some real-world applications of scaling down objects, such as in model making or map creation?" |
Proportions |
|
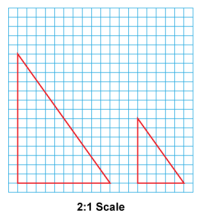
Math Clip Art--Geometry Concepts--Scale Drawing--08 | Math Clip Art--Scale Drawing--08TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a right triangle that has been scaled down by a factor of 2:1. Each side of the triangle in the drawing is one-half the length of the corresponding side in the actual object. This scaling helps in visualizing smaller versions of objects while maintaining accurate proportions. Teacher's Script: "Observe this scale drawing of a right triangle. How does the 2:1 scale factor affect the dimensions of the drawing compared to the actual triangle? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
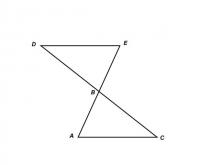
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
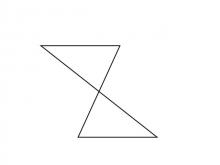
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
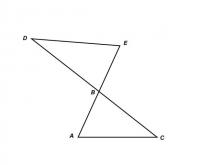
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
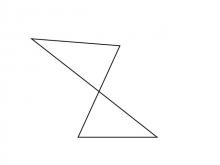
Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles Share Vertical Angles Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
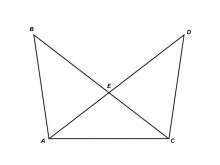
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
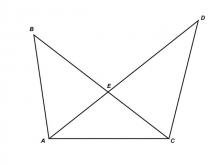
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |

|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
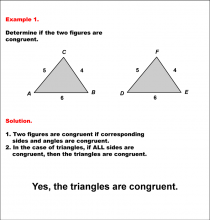
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
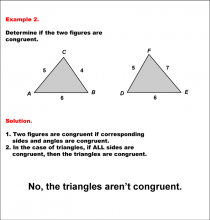
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
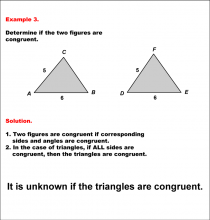
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |