Display Title
Definition | 3D Geometry Concepts | Cross-Sections of a Sphere
Display Title
Cross Sections of a Sphere

Topic
3D Geometry
Definition
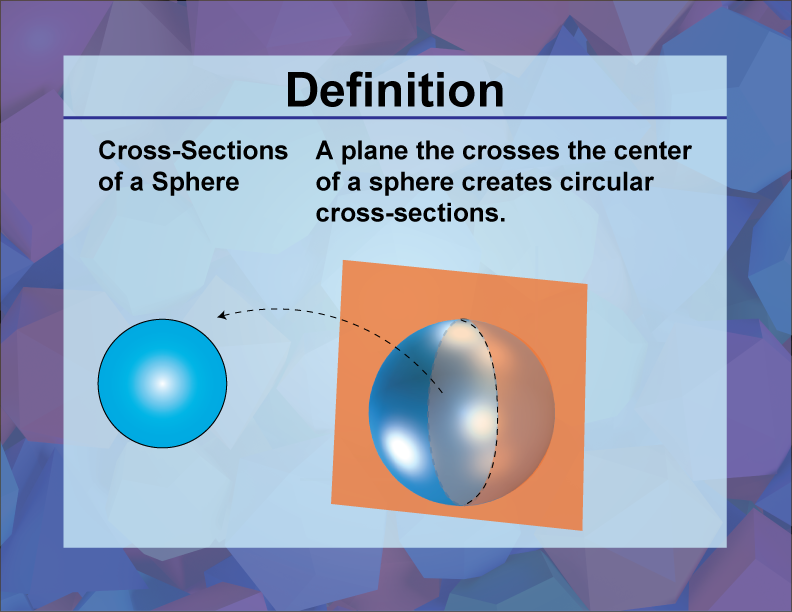
A cross-section of a sphere is the intersection of a plane with the sphere, resulting in a circle.
Description
In three-dimensional geometry, understanding the concept of cross-sections is crucial for visualizing and analyzing the properties of various 3D shapes. A sphere, which is a perfectly round geometrical object in three-dimensional space, can be intersected by a plane in various ways. When a plane cuts through a sphere, the shape of the intersection is always a circle. The size of this circle depends on the position of the plane relative to the center of the sphere.
If the plane passes through the center of the sphere, the resulting cross-section is a great circle, which is the largest possible circle that can be drawn on the sphere. Great circles are significant in various fields such as geography and astronomy because they represent the shortest path between two points on the surface of a sphere. On the other hand, if the plane intersects the sphere at any other point, the cross-section is a smaller circle. These smaller circles are vital in different applications, including engineering and computer graphics, where understanding the spatial relationships and properties of spherical objects is essential.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3, CCSS.MATH.CONTENT.7.G.A.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • Spheres |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |