Display Title
Definition | 3D Geometry Concepts | Horizontal Cross-Sections of a Cylinder
Display Title
Horizontal Cross Sections of a Cylinder

Topic
3D Geometry
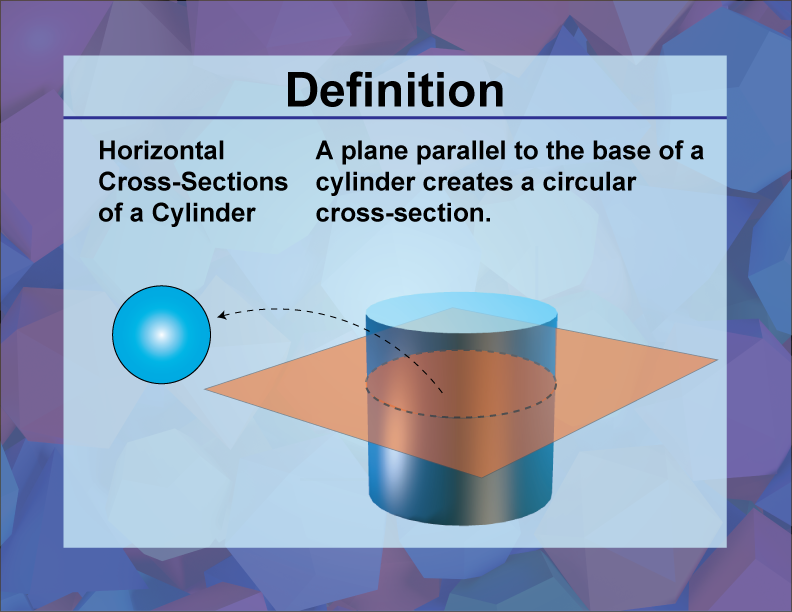
Definition
A horizontal cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to the base of the cylinder.
Description
In the context of three-dimensional geometry, understanding the concept of cross-sections is crucial. A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. When a horizontal plane intersects a cylinder, the resulting cross-section is a circle. This concept is not only fundamental in geometry but also has practical applications in various fields.
In architecture and engineering, horizontal cross-sections of cylindrical structures help in visualizing and designing components like pipes, tunnels, and columns. In medical imaging, techniques like CT scans utilize cross-sectional views to examine the interior of cylindrical body parts, such as blood vessels and bones, providing critical information for diagnosis and treatment.
Understanding the properties of these cross-sections aids in calculating the surface area and volume of cylinders, which are essential for material estimation and structural analysis. This geometric principle also extends to other shapes, providing a foundational tool for analyzing and interpreting three-dimensional objects in various scientific and practical applications.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3, CCSS.MATH.CONTENT.7.G.A.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • Cylinders |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term, cylinder |