Display Title
Definition | 3D Geometry Concepts | Net for a Cube
Display Title
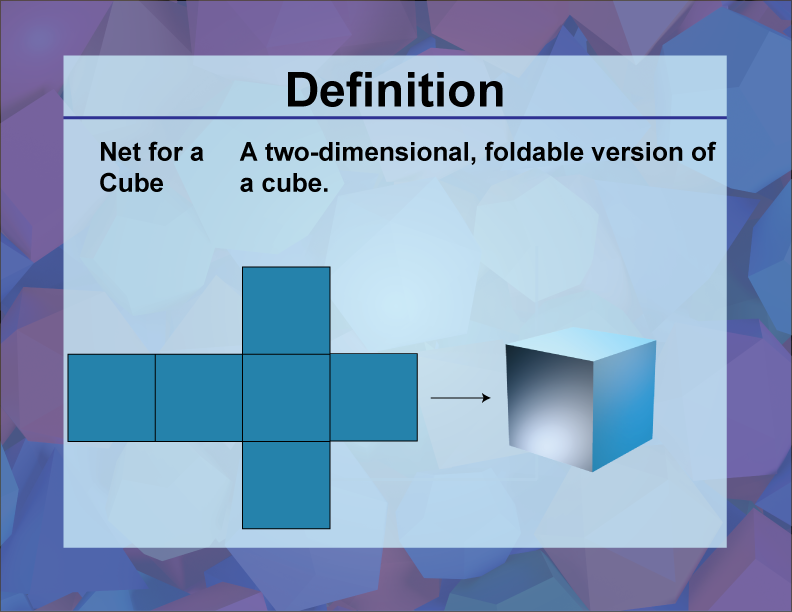
Net for a Cube

Topic
3D Geometry
Definition
A net for a cube is a two-dimensional shape that can be folded to form a three-dimensional cube.
Description
In the realm of three-dimensional geometry, a net for a cube is a crucial concept. It represents a flattened out three-dimensional shape that can be folded along the edges to form a cube. This is an essential tool for visualizing and understanding how 3D shapes are constructed from 2D representations.
A cube is a regular polyhedron with six identical square faces, twelve edges, and eight vertices. The net of a cube consists of six squares arranged in such a way that they can be folded along their edges to create the three-dimensional shape of a cube. There are 11 different nets that can form a cube, each demonstrating the versatility and complexity of geometric transformations.
Understanding the net of a cube is fundamental in various applications, including architecture, packaging, and manufacturing, where it is essential to visualize and manipulate three-dimensional objects from their two-dimensional plans. It also plays a significant role in mathematical education, helping students grasp the concept of three-dimensional space and the relationships between different geometric shapes.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • Cubes |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |