Display Title
Definition | 3D Geometry Concepts | Net for an Octahedron
Display Title
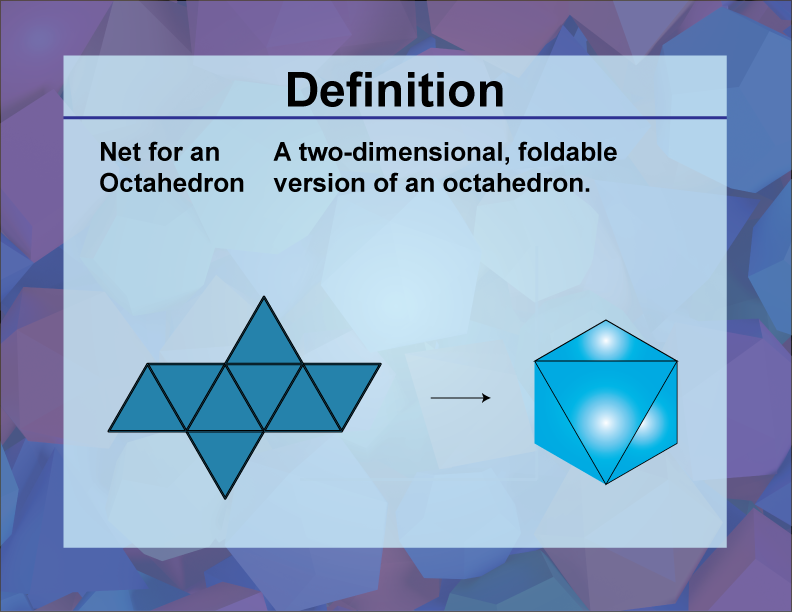
Net for an Octahedron

Topic
3D Geometry
Definition
A net for an octahedron is a two-dimensional figure that can be folded to form a three-dimensional octahedron.
Description
In the realm of three-dimensional geometry, a net is a crucial concept that helps in visualizing and constructing 3D shapes from 2D representations. Specifically, a net for an octahedron consists of eight equilateral triangles arranged in a specific pattern. When these triangles are folded along the edges, they form an octahedron, which is a polyhedron with eight faces, twelve edges, and six vertices.
The relevance of understanding nets in 3D geometry extends beyond simple visualization. It aids in comprehending the properties and relationships between different geometric shapes. For instance, by studying the net of an octahedron, one can better understand the symmetry and surface area of the shape. This knowledge is particularly useful in fields such as architecture, engineering, and various branches of science where spatial reasoning is essential.
Moreover, nets are instrumental in educational settings as they provide a hands-on approach to learning geometry. They allow students to physically manipulate shapes, fostering a deeper understanding of geometric concepts. The net for an octahedron, with its symmetrical and uniform structure, serves as an excellent example of how complex 3D shapes can be broken down into simpler 2D components.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • 3-Dimensional Figures |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |