Display Title
Definition | 3D Geometry Concepts | Net for a Tetrahedron
Display Title
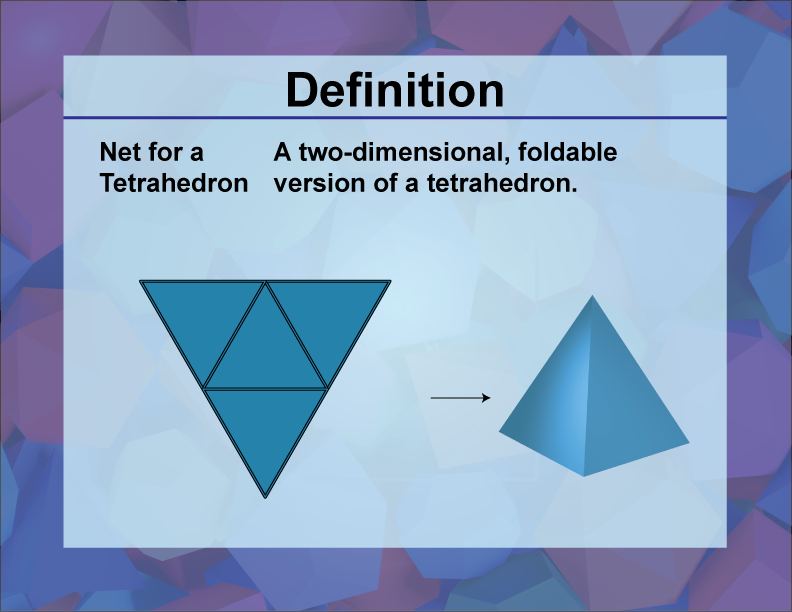
Net for a Tetrahedron

Topic
3D Geometry
Definition
A net for a tetrahedron is a two-dimensional pattern that can be folded to form a three-dimensional tetrahedron, which is a polyhedron with four triangular faces.
Description
In the realm of three-dimensional geometry, the concept of a net is crucial for understanding the structure and properties of polyhedra. A tetrahedron, one of the simplest forms of polyhedra, consists of four triangular faces, six edges, and four vertices. The net of a tetrahedron is a flat, two-dimensional figure that, when folded along its edges, forms the three-dimensional shape of the tetrahedron.
The net of a tetrahedron is particularly significant in educational contexts, as it helps students visualize and comprehend the transition from two-dimensional shapes to three-dimensional structures. By studying the net, learners can better understand the spatial relationships and geometric properties that define the tetrahedron. This understanding is foundational for more complex studies in geometry, such as calculating surface areas and volumes of polyhedra.
In practical applications, nets are used in various fields including architecture, engineering, and computer graphics. For instance, architects and engineers use nets to design and visualize structures before they are built, ensuring that all components fit together correctly. In computer graphics, nets are used to create 3D models for animation and virtual reality environments, enhancing the realism and functionality of digital designs.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • 3-Dimensional Figures |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |