Display Title
Definition | 3D Geometry Concepts | Slant Height
Display Title
Slant Height

Topic
3D Geometry
Definition
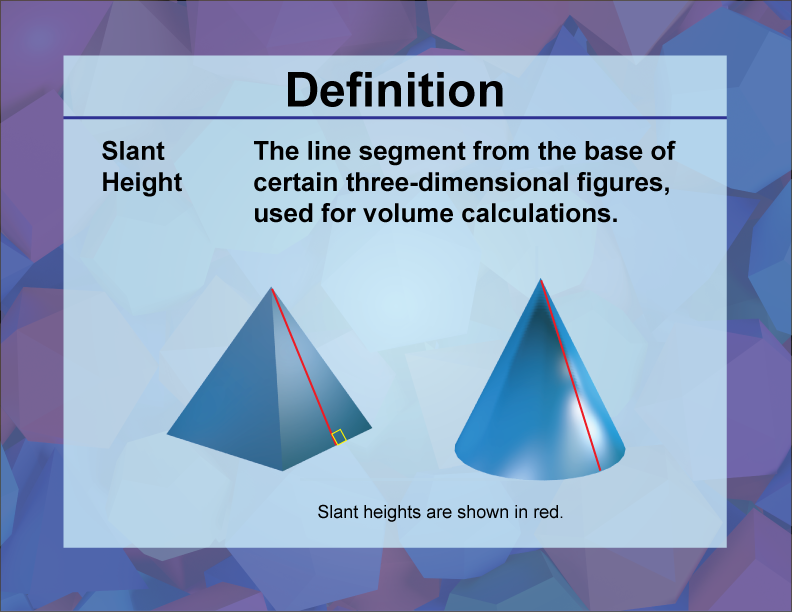
Slant height is the distance measured along a lateral face from the base to the apex of a three-dimensional figure, such as a pyramid or a cone.
Description
In the context of three-dimensional geometry, the slant height is a crucial measurement for various solid figures, particularly right pyramids and right circular cones. It represents the shortest path along the surface of the figure from the apex (top point) to the base, distinguishing it from the vertical height which measures the perpendicular distance from the apex to the center of the base.
Understanding the slant height is essential for calculating the surface area and volume of these solids. For instance, in a right circular cone, the slant height can be determined using the Pythagorean theorem, where the slant height forms the hypotenuse of a right triangle, with the radius of the base and the vertical height as the other two sides. The formula is given by $$l = \sqrt{r^2 + h^2}$$where l is the slant height, r is the radius, and h is the vertical height.
In practical applications, the slant height is used in various fields such as architecture and engineering to design and construct structures like conical roofs and pyramidal towers. It also plays a role in manufacturing processes where precise measurements are required to create components that fit together seamlessly.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • 3-Dimensional Figures |
| Copyright Year | 2013 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |