Display Title
Definition | 3D Geometry Concepts | Vertical Cross-Sections of a Triangular Prism
Display Title
Vertical Cross Sections of a Triangular Prism
Topic
3D Geometry
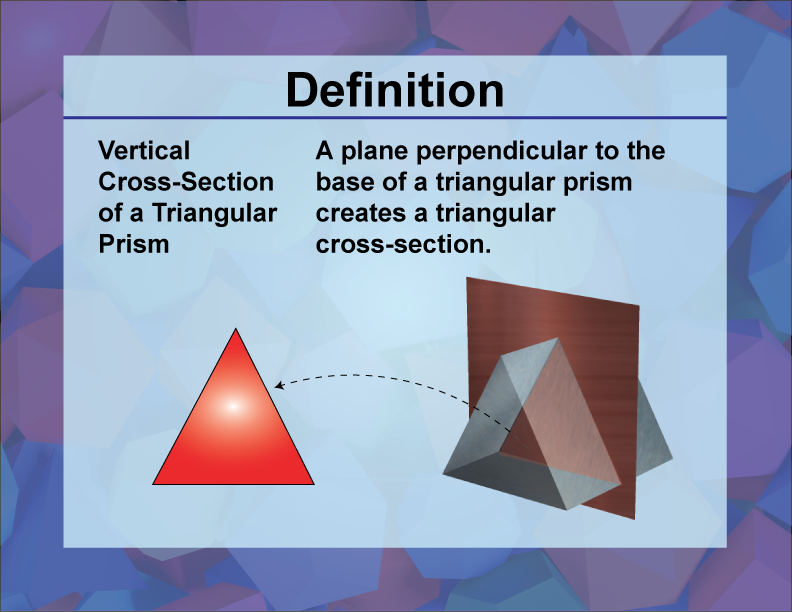
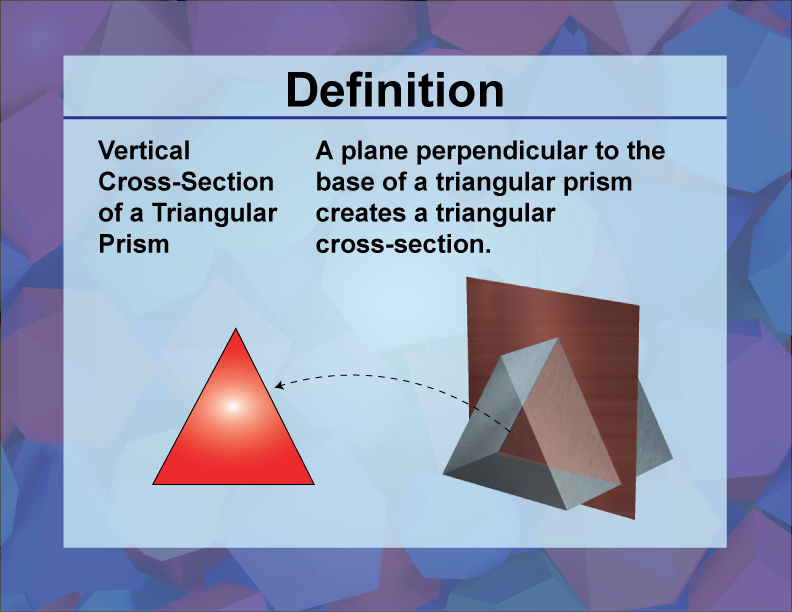
Definition
A vertical cross section of a triangular prism is a two-dimensional shape obtained by slicing the prism parallel to its height, revealing a triangular face.
Description
In the realm of three-dimensional geometry, understanding cross sections is crucial for visualizing and analyzing the internal structure of 3D shapes. A triangular prism is a polyhedron with two parallel, congruent triangular bases connected by rectangular faces. When a vertical plane slices through a triangular prism parallel to its height, the resulting cross section is a triangle, identical to the triangular sides of the prism.
Vertical cross sections are particularly significant in various applications of 3D geometry. For instance, in engineering and architecture, cross-sectional views are essential for structural analysis and design. They help engineers understand the internal components and load distribution within a structure. In manufacturing, cross sections allow for precise material cutting and assembly processes.
Moreover, vertical cross sections aid in educational contexts, providing students with a tangible understanding of how 3D objects can be dissected into 2D shapes. This concept is fundamental in fields like calculus, where cross sections are used to compute volumes and surface areas of complex solids through integral calculus.
Understanding the vertical cross sections of a triangular prism not only enhances spatial reasoning but also bridges the gap between theoretical geometry and practical applications, making it an indispensable concept in both academic and professional settings.
For a complete collection of terms related to 3D geometry click on this link: 3D Collection.
| Common Core Standards | CCSS.MATH.CONTENT.5.MD.C.3, CCSS.MATH.CONTENT.7.G.A.3 |
|---|---|
| Grade Range | 4 - 6 |
| Curriculum Nodes |
Geometry • 3D Geometry • Triangular Prisms |
| Copyright Year | 2021 |
| Keywords | three-dimensional geometry, 3d Geometry, defnitions, glossary term |