Display Title
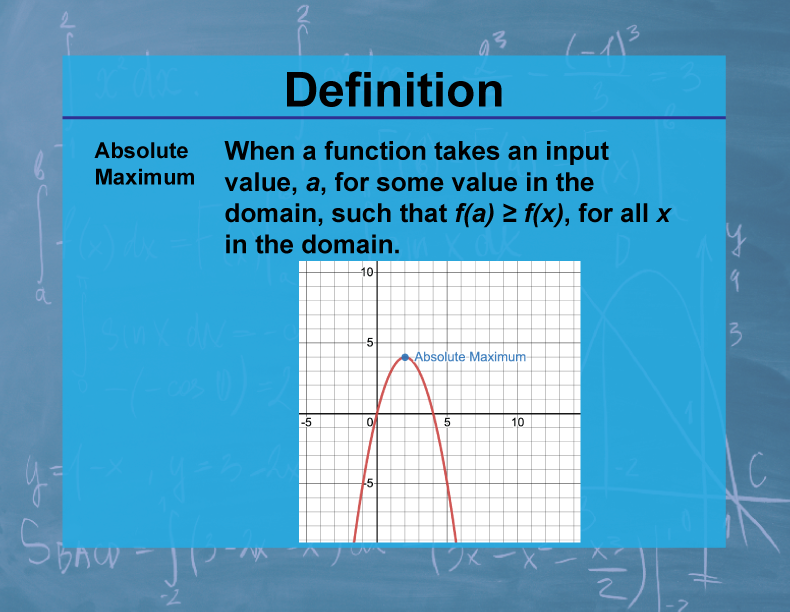
Definition--Calculus Topics--Absolute Maximum
Display Title
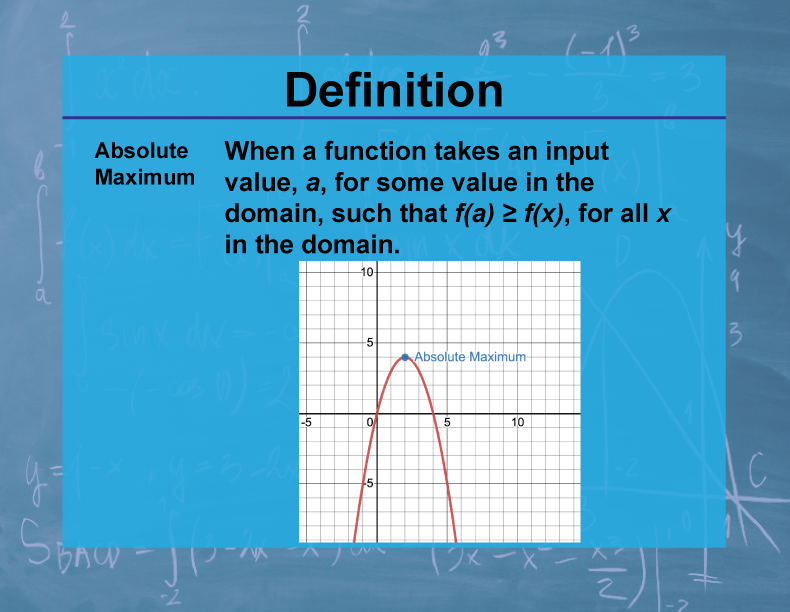
Definition--Calculus Topics--Absolute Maximum
Topic
Calculus
Definition
The absolute maximum of a function is the largest value the function attains over its entire domain. It represents the highest point on the graph of the function.
Description
The concept of absolute maximum is crucial in calculus as it helps us understand the behavior of functions and their extrema. In real-world applications, absolute maxima are used to optimize processes, maximize profits, or determine the highest point of a structure. For instance, in business, finding the absolute maximum of a profit function can help determine the optimal price point for a product.
In mathematics education, understanding absolute maxima is essential for grasping function behavior, optimization problems, and the foundations of calculus. It introduces students to the idea that functions can have global extrema, which is different from local extrema. This concept is particularly important when studying continuous functions on closed intervals, as the Extreme Value Theorem guarantees the existence of absolute extrema in such cases.
Teacher's Script: "Imagine you're designing a roller coaster. The absolute maximum of your height function would represent the highest point of the entire ride. Let's say our function is h(t) = -t2 + 10t, where t is the time in seconds and h is the height in meters. To find the absolute maximum, we can use calculus techniques like finding critical points and evaluating endpoints. This highest point is crucial for safety regulations and thrill factor!"

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |