Display Title
Definition--Calculus Topics--Absolute Minimum
Display Title
Definition--Calculus Topics--Absolute Minimum

Topic
Calculus
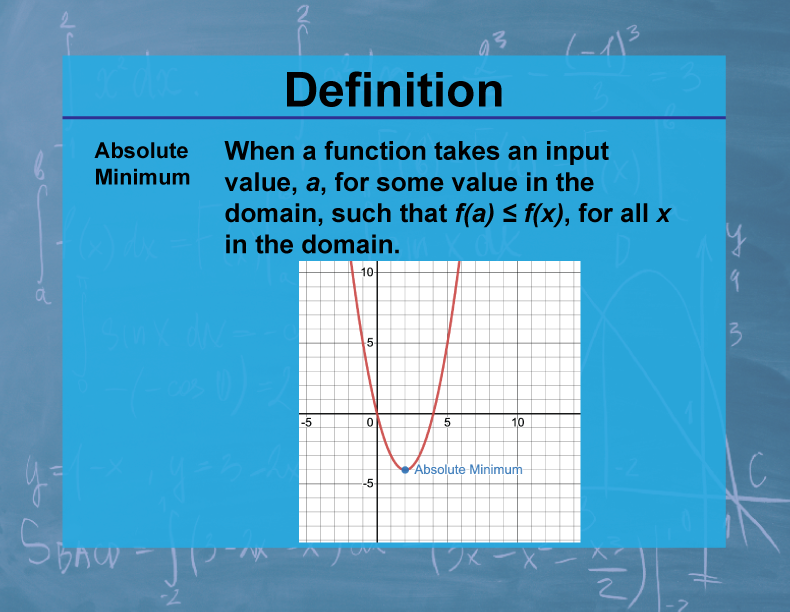
Definition
The absolute minimum of a function is the smallest value the function attains over its entire domain. It represents the lowest point on the graph of the function.
Description
Understanding the absolute minimum is essential in calculus as it helps us analyze function behavior and solve optimization problems. In real-world applications, finding the absolute minimum is crucial for minimizing costs, reducing energy consumption, or determining the most efficient use of resources. For example, in manufacturing, identifying the absolute minimum of a cost function can help determine the most cost-effective production method.
In mathematics education, the concept of absolute minimum is fundamental to understanding function analysis and optimization techniques. It introduces students to the idea of global extrema and how they differ from local extrema. This concept is particularly important when studying continuous functions on closed intervals, as the Extreme Value Theorem guarantees the existence of absolute extrema in such cases.
Teacher's Script: "Let's consider a practical example. Imagine you're designing a package for a product, and you want to minimize the amount of material used. If we represent the surface area of the package as a function of its dimensions, finding the absolute minimum of this function will give us the most efficient design. We can use calculus techniques to find the value of x that gives us the absolute minimum surface area."

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |