Display Title
Definition--Calculus Topics--Continuous Functions
Display Title
Definition--Calculus Topics--Continuous Functions
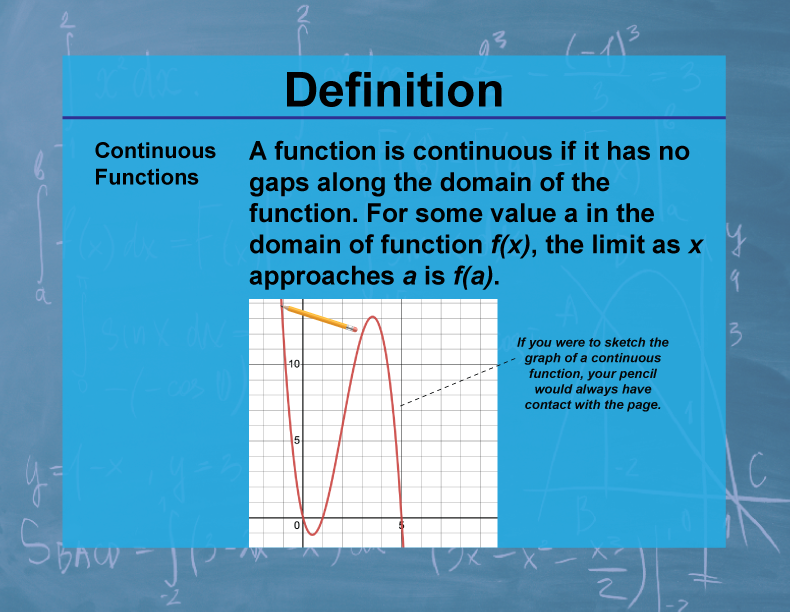
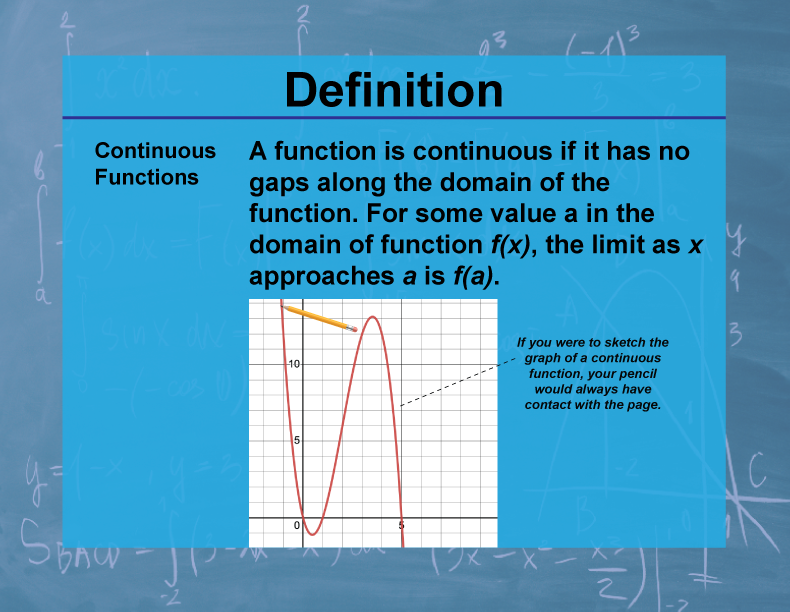
Definition--Calculus Topics--Continuous Functions
A function is continuous if it has no gaps along the domain of the function. For some value a in the domain of function f(x), the limit as x approaches a is f(a).
— CLICK THE PREVIEW BUTTON TO SEE THE DEFINITION CARD —
To see the complete collection of Calculus terms, click on this link.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |