Display Title
Definition--Calculus Topics--Convex Function
Display Title
Definition--Calculus Topics--Convex Function
Topic
Calculus
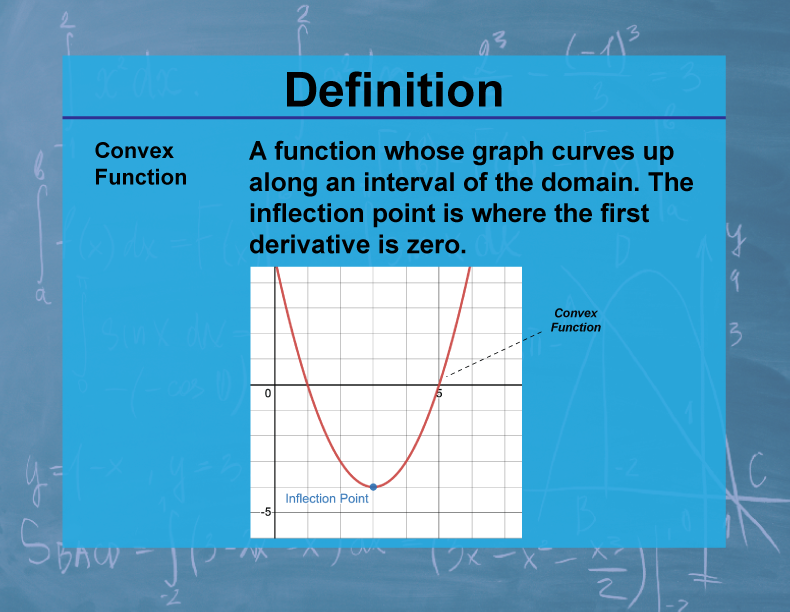
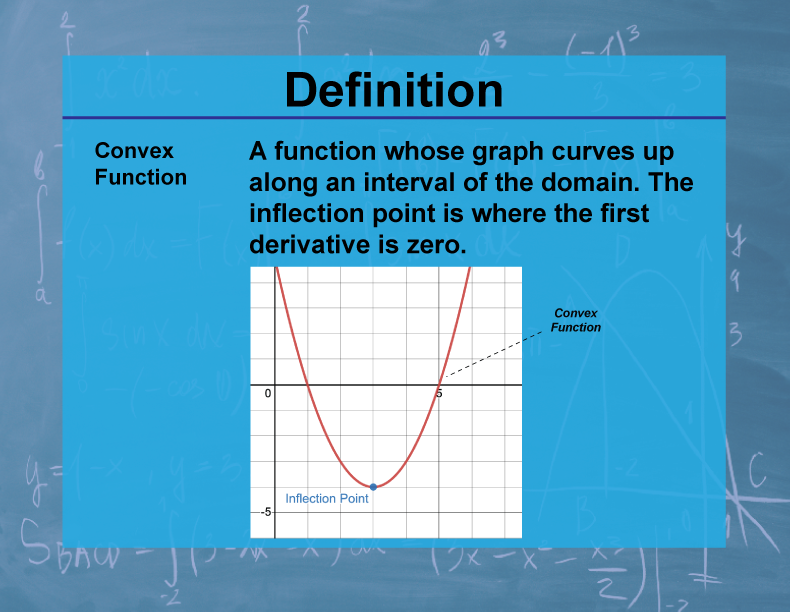
Definition
A function is convex on an interval if the line segment between any two points on the graph of the function lies above or on the graph.
Description
Convex functions play a crucial role in calculus and optimization theory. In real-world applications, convex functions are often used to model phenomena where the rate of change is increasing, such as in economics for modeling increasing marginal costs or in physics for describing certain types of potential energy. Understanding convexity is essential for solving minimization problems and analyzing function behavior.
In mathematics education, the concept of convex functions helps students develop a deeper understanding of function behavior and its graphical representation. It's crucial for teaching optimization techniques and the second derivative test. This concept bridges the gap between visual intuition and rigorous mathematical analysis, enhancing students' problem-solving skills in calculus and its applications in various fields.
Teacher's Script: "Imagine you're running a business and plotting your average cost per unit as you produce more items. Initially, your costs decrease as you benefit from economies of scale. But after a certain point, your costs start to increase again due to factors like increased complexity. This U-shaped curve is a perfect example of a convex function. Can you think of other real-world scenarios where we might encounter convex functions? How about the relationship between study time and test scores after a certain point of diminishing returns?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |