Display Title
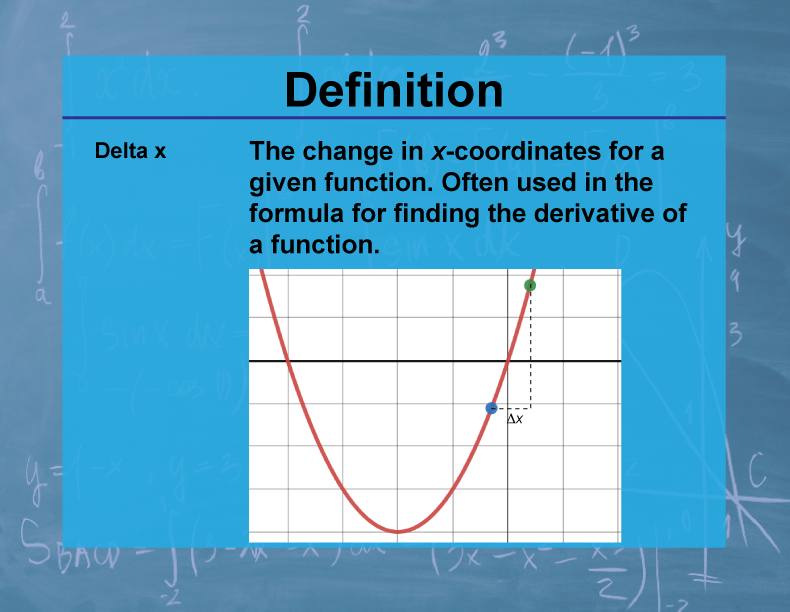
Definition--Calculus Topics--Delta x
Display Title
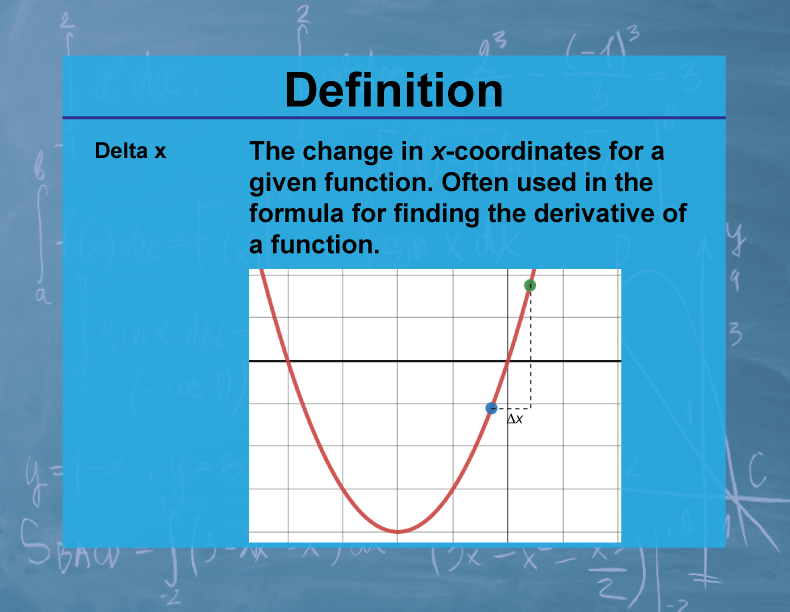
Definition--Calculus Topics--Delta x
Topic
Calculus
Definition
Delta x (Δx) represents the change in the x-coordinate between two points on a function. It is calculated as the difference between the final x-value and the initial x-value: Δx = x₂ - x₁.
Description
Delta x is a fundamental concept in calculus, particularly in understanding rates of change and limits. It's crucial in the definition of derivatives and integrals, forming the basis for many calculus operations. In real-world applications, Delta x is used to model small changes or increments in various fields, such as physics (for displacement), economics (for marginal analysis), and engineering (for error analysis).
In mathematics education, Delta x helps students transition from algebra to calculus by introducing the idea of small changes and their effects. It's essential for developing intuition about limits and continuity, and it provides a concrete way to visualize the process of taking a derivative or constructing a Riemann sum for integration.
Teacher's Script: "Imagine you're tracking the position of a car. At time t₁ = 2 seconds, the car is at x₁ = 10 meters, and at t₂ = 5 seconds, it's at x₂ = 25 meters. The Delta x here would be 25 - 10 = 15 meters. This tells us how far the car moved in that time interval. Now, if we divide Delta x by the change in time (Delta t), what would that give us? That's right, the average velocity! Can you see how Delta x is crucial in understanding motion and rates of change?"

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |