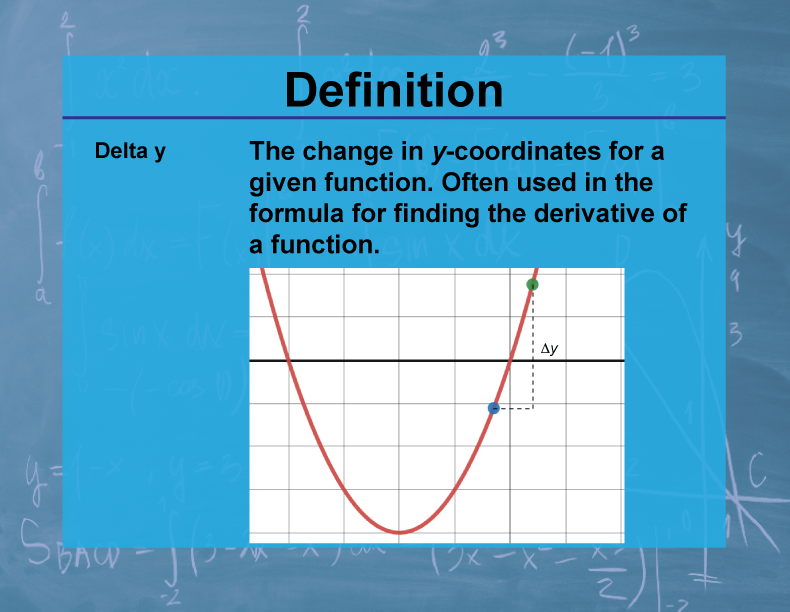
Definition--Calculus Topics--Delta y
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Advanced Topics in Algebra >> Calculus Vocabulary

Definition--Calculus Topics--Delta y

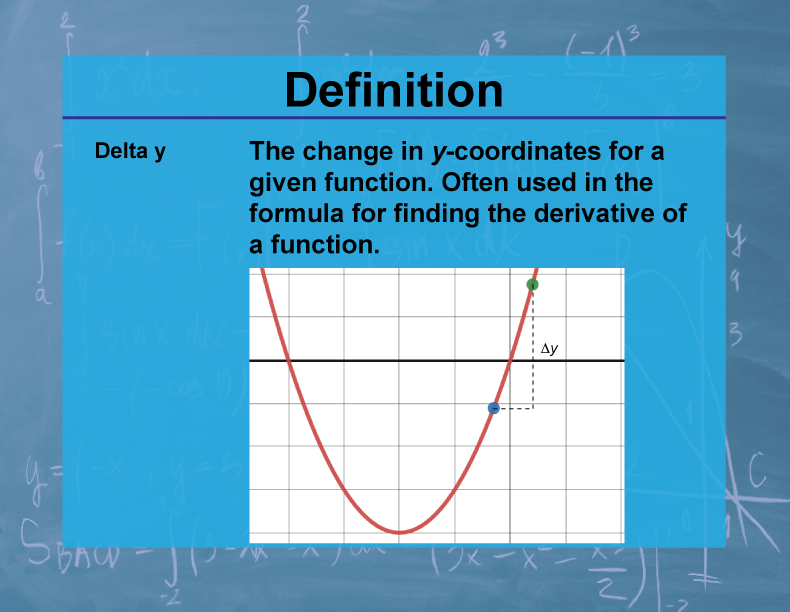
Definition--Calculus Topics--Delta y

The change in y-coordinates for a given function. Often used in the formula for finding the derivative of a function.

— CLICK THE PREVIEW BUTTON TO SEE THE DEFINITION CARD —

To see the complete collection of Calculus terms, click on this link.

Grade Range 11 - 12
Curriculum Nodes Algebra
    • Advanced Topics in Algebra
        • Calculus Vocabulary
Copyright Year 2023
Keywords calculus concepts, limits, derivatives, integrals, composite functions