Display Title
Definition--Calculus Topics--Derivative of a Linear Function
Display Title
Definition--Calculus Topics--Derivative of a Linear Function
Topic
Calculus
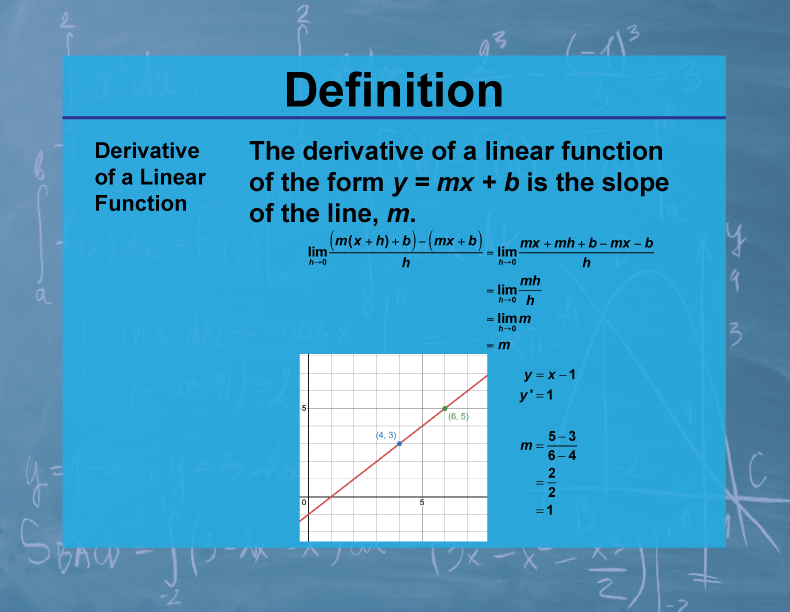
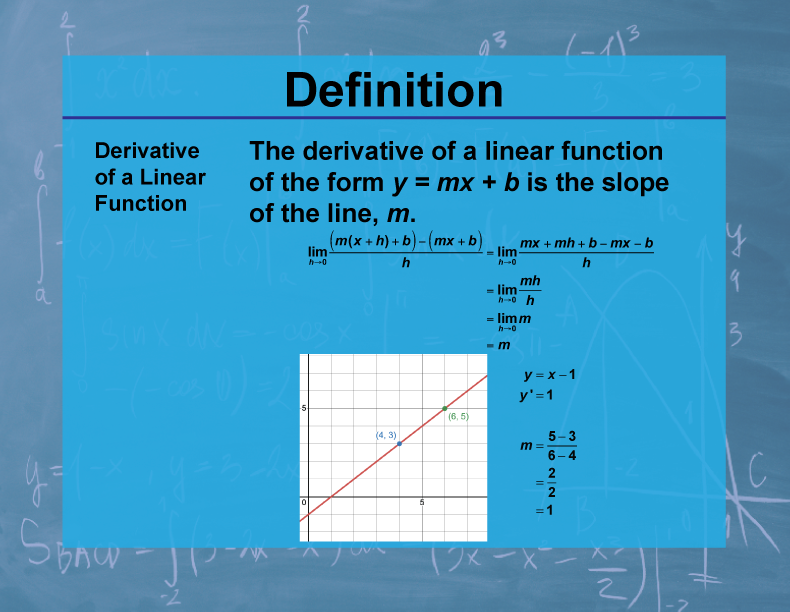
Definition
The derivative of a linear function f(x) = mx + b is a constant function f'(x) = m, where m is the slope of the linear function.
Description
The derivative of a linear function is a fundamental concept in calculus that illustrates the relationship between a function's rate of change and its graphical representation. In real-world applications, this concept is used in physics to describe constant velocity, in economics to model constant marginal costs or revenues, and in engineering for linear approximations of more complex systems.
In mathematics education, understanding the derivative of a linear function helps students grasp the connection between slopes in algebra and rates of change in calculus. It serves as a simple yet powerful example of how derivatives work, providing a foundation for understanding more complex function derivatives. This concept is crucial for developing students' intuition about the meaning of derivatives and their graphical interpretation.
Teacher's Script: "Imagine you're filling a swimming pool at a constant rate of 50 liters per minute. The volume (V) of water in the pool after t minutes can be represented by the function V(t) = 50t + 1000, where 1000 is the initial volume in liters. What's the derivative of this function? That's right, V'(t) = 50. This constant derivative tells us that the rate of change of the volume is always 50 liters per minute, regardless of time. Can you think of other real-life scenarios where we might encounter linear functions and constant rates of change?"

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |