Display Title
Definition--Calculus Topics--Differentiable Function
Display Title
Definition--Calculus Topics--Differentiable Function
Topic
Calculus
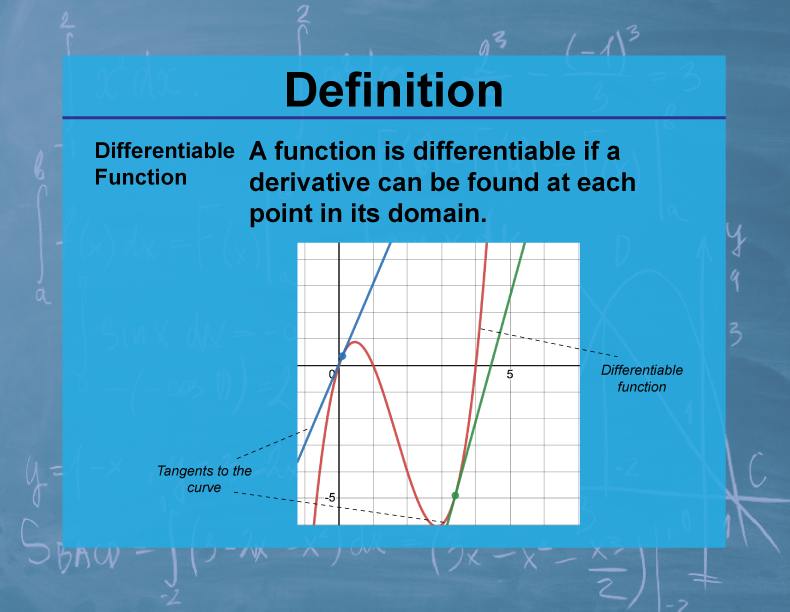
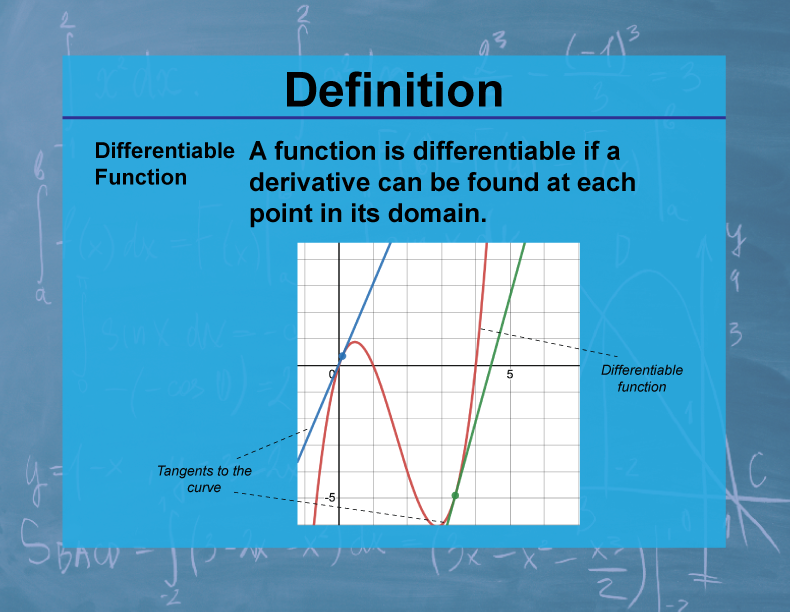
Definition
A function is differentiable at a point if it has a derivative at that point. This means the function is continuous at that point and has a well-defined tangent line.
Description
The concept of differentiable functions is fundamental in calculus and has wide-ranging applications in physics, engineering, and economics. Differentiable functions are crucial for modeling smooth changes in physical systems, optimizing processes, and analyzing rates of change. In real-world applications, differentiability ensures that small changes in input produce predictable changes in output, which is essential for many mathematical models.
In mathematics education, understanding differentiable functions helps students grasp the connection between continuity and smoothness of functions. It's a key concept for developing intuition about function behavior and is essential for applying calculus techniques to solve real-world problems. This concept also introduces students to the limitations of differentiation and helps them recognize when calculus techniques can be applied.
Teacher's Script: "Let's consider a company's profit function P(x) = x3 - 3x2 + 2x, where x is the number of units produced. This function is differentiable for all real numbers. What does this tell us about the company's profit? It means we can find the rate of change of profit with respect to production at any point. We can use this to find the optimal production level for maximum profit. Now, consider a function like f(x) = |x|. Is this differentiable everywhere? Why or why not? How does this affect our ability to analyze it?"

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |