Display Title
Definition--Calculus Topics--Discontinuous Function
Display Title
Definition--Calculus Topics--Discontinuous Function
Topic
Calculus
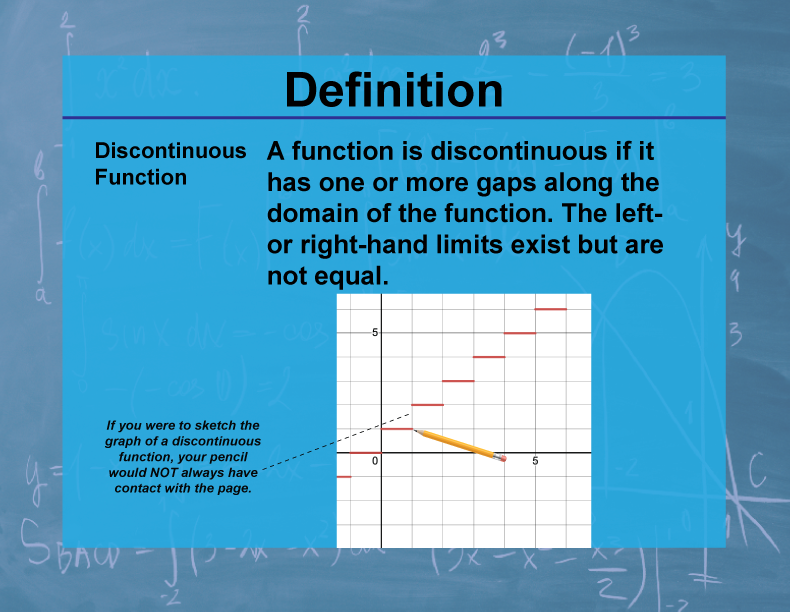
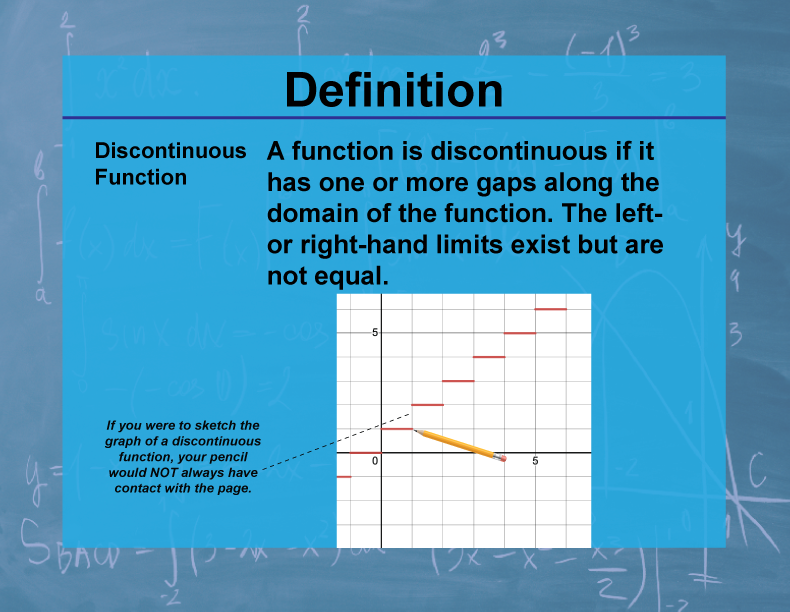
Definition
A discontinuous function is a function that is not continuous at one or more points in its domain. It has a break, jump, or hole in its graph.
Description
Discontinuous functions are important in calculus as they represent situations where smooth, continuous change is interrupted. They occur in various real-world scenarios, such as step functions in economics (tax brackets), piecewise functions in physics (phase transitions), and in signal processing (digital signals). Understanding discontinuities is crucial for analyzing function behavior and determining where calculus techniques can be applied.
In mathematics education, studying discontinuous functions helps students develop a deeper understanding of function behavior and limits. It challenges the intuition built from working with continuous functions and prepares students for more advanced topics in calculus and analysis. Recognizing and classifying different types of discontinuities (removable, jump, infinite) is an important skill for students pursuing studies in mathematics, physics, or engineering.
Teacher's Script: "Let's consider a real-world example of a discontinuous function. Imagine a taxi fare structure where the first mile costs $5, and each additional mile costs $2. How would we represent this as a function? It would be a piecewise function with a jump discontinuity at x = 1. Can you sketch this function? How does this discontinuity affect the total fare? What implications does this have for passengers and taxi companies? Can you think of other real-world scenarios where we might encounter discontinuous functions?"

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |