Display Title
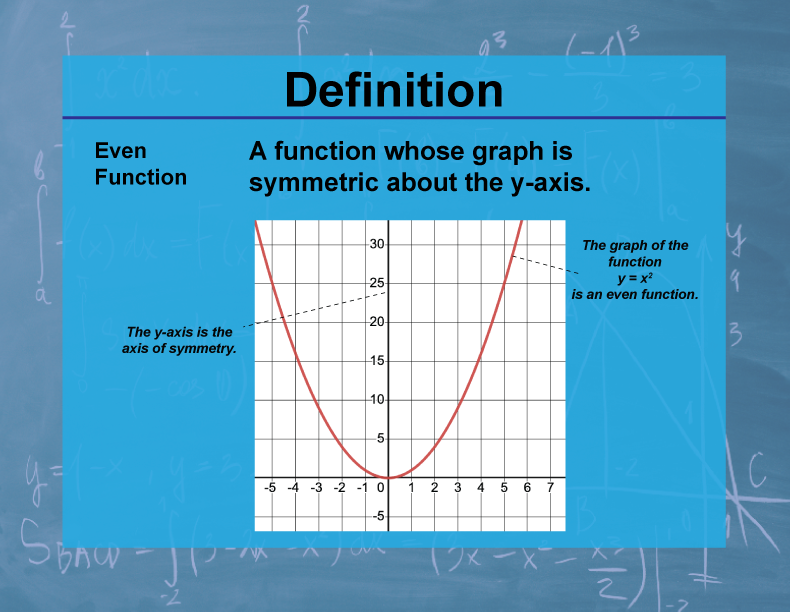
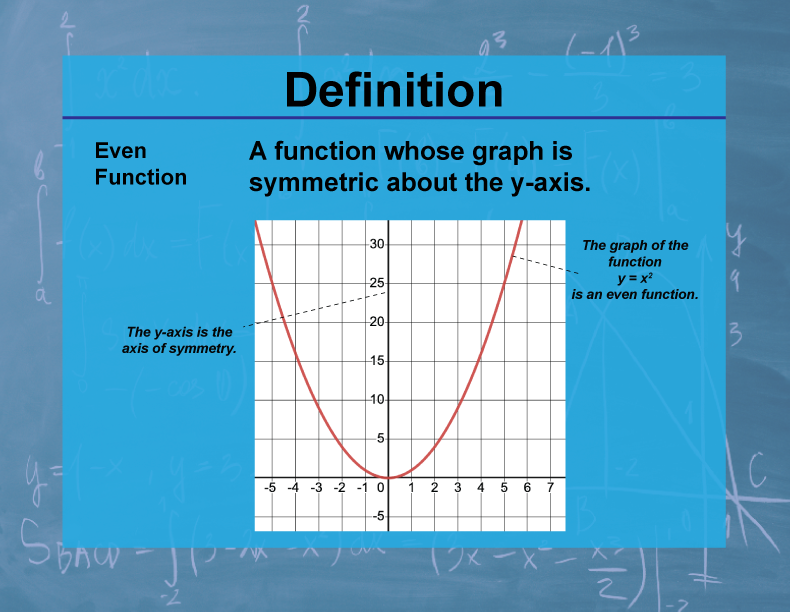
Definition--Calculus Topics--Even Function
Display Title
Definition--Calculus Topics--Even Function
Topic
Calculus
Definition
An even function is a function that is symmetric about the y-axis. Mathematically, a function f(x) is even if f(-x) = f(x) for all x in the domain of f.
Description
Even functions play a significant role in calculus and many areas of mathematics and physics. Their symmetry property makes them particularly useful in modeling physical phenomena that exhibit symmetrical behavior, such as the motion of a simple pendulum or the shape of certain wave functions in quantum mechanics. In calculus, even functions have special properties with respect to integration and differentiation, which can simplify calculations and lead to important insights.
In mathematics education, the concept of even functions helps students develop a deeper understanding of function symmetry and its implications. It's an important tool for analyzing and graphing functions, and it provides a foundation for more advanced topics such as Fourier series in higher mathematics. Understanding even functions also enhances students' ability to recognize patterns and symmetries in mathematical expressions and real-world phenomena.
Teacher's Script: "Let's consider the function f(x) = x2. If we input any number and its negative, like 3 and -3, we get the same output: f(3) = 9 and f(-3) = 9. This symmetry is what makes it an even function. Now, let's graph it. Notice how the graph is a perfect mirror image if we fold it along the y-axis. Can you think of other functions that might have this property? How about cos(x) or |x|? How does this symmetry affect the area under the curve when we integrate an even function from -a to a?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |