Display Title
Definition--Calculus Topics--Extreme Value Theorem
Display Title
Definition--Calculus Topics--Extreme Value Theorem
Topic
Calculus
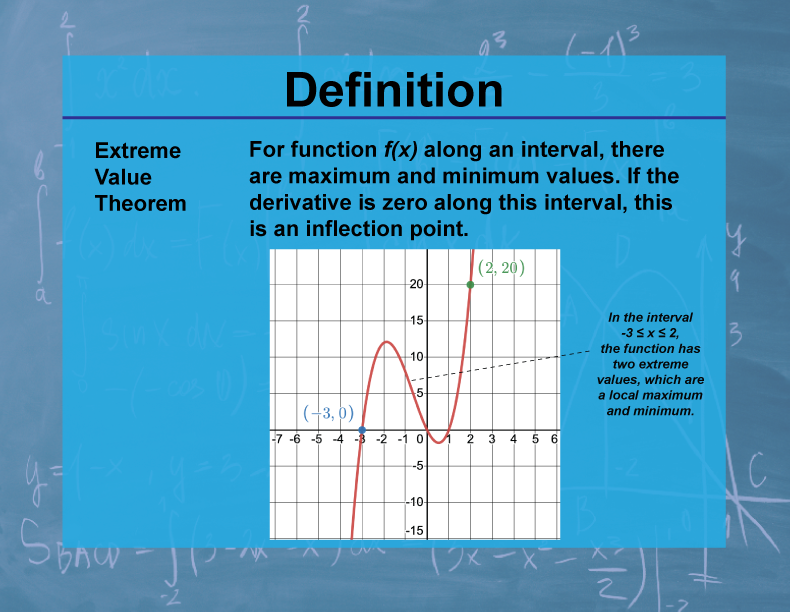
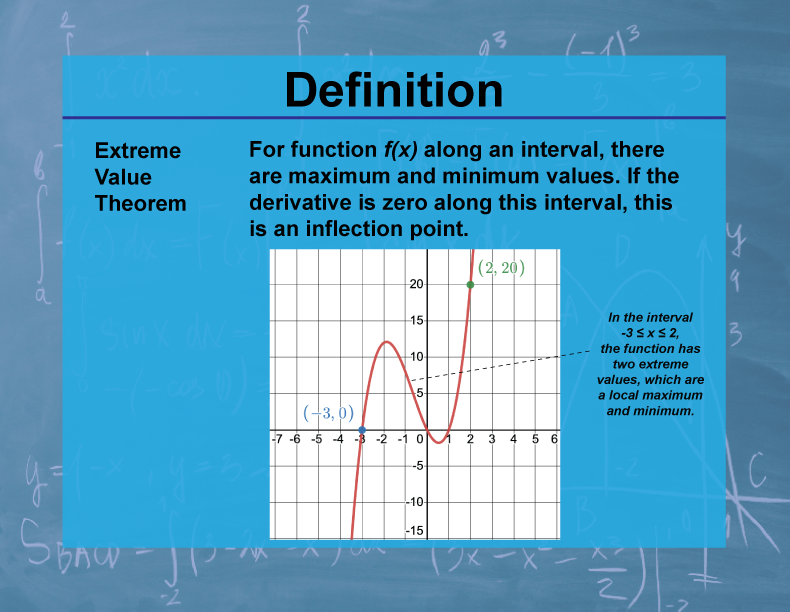
Definition
The Extreme Value Theorem states that if a function f is continuous on a closed interval [a,b], then f attains both a maximum and a minimum value on that interval.
Description
The Extreme Value Theorem is a fundamental result in calculus with significant implications for optimization problems in various fields. It guarantees the existence of maximum and minimum values for continuous functions on closed intervals, which is crucial in many real-world applications. In economics, it's used to find optimal prices or production levels; in engineering, it helps in designing efficient systems; and in physics, it's applied to find equilibrium states.
In mathematics education, the Extreme Value Theorem helps students understand the behavior of continuous functions and the importance of domain restrictions. It bridges the gap between intuitive understanding of maxima and minima and rigorous mathematical proofs. This theorem is also a stepping stone to more advanced concepts in analysis and provides a foundation for optimization techniques in calculus.
Teacher's Script: "Imagine you're designing a box with a fixed surface area. The Extreme Value Theorem tells us that there must be a maximum volume this box can have. But how do we find it? This is where calculus comes in. We can use derivatives to find critical points, and the Extreme Value Theorem guarantees that our maximum must occur at one of these points or at the endpoints of our interval. Let's work through this problem step by step, and then discuss how this theorem applies to other real-world scenarios, like finding the most efficient shape for a soda can or optimizing the profit of a business."

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |