Display Title
Definition--Calculus Topics--First Derivative
Display Title
Definition--Calculus Topics--First Derivative
Topic
Calculus
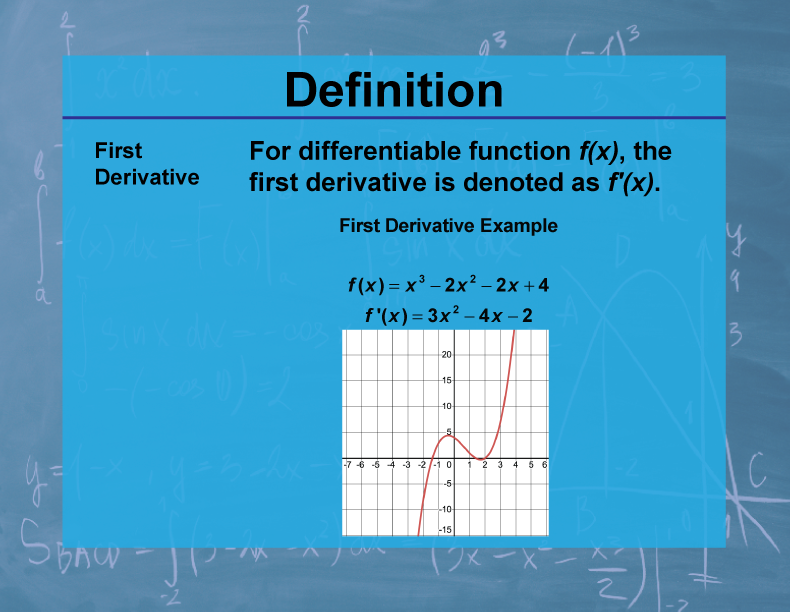
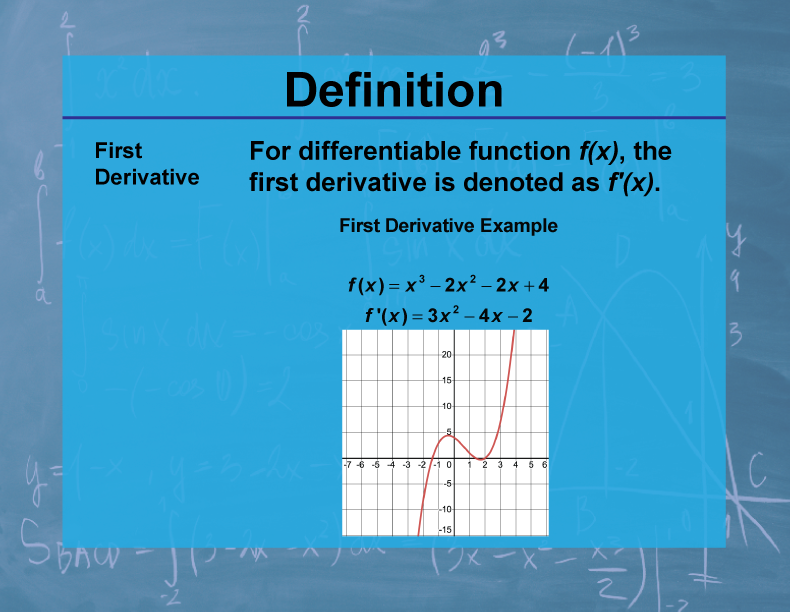
Definition
The first derivative of a function f(x), denoted as f'(x), represents the rate of change of the function with respect to its variable. It is defined as the limit of the difference quotient as the change in x approaches zero.
Description
The first derivative is a fundamental concept in calculus, providing crucial information about the behavior of functions. In physics, it represents velocity when the function describes position; in economics, it can represent marginal cost or marginal revenue. The first derivative is used to find the slope of a tangent line to a curve at any point, helping to analyze the function's rate of change, direction of growth, and critical points.
In mathematics education, understanding the first derivative helps students transition from average rates of change to instantaneous rates of change. It's essential for graphing functions, solving optimization problems, and understanding the concept of linearization. The first derivative also serves as a foundation for higher-order derivatives and more advanced calculus concepts.
Teacher's Script: "Let's consider a function that represents the position of a car over time, s(t) = t2 + 2t. The first derivative, s'(t) = 2t + 2, gives us the car's velocity at any time t. How can we interpret this? At t = 0, the velocity is 2 m/s, and it's increasing over time. Where is the car's velocity zero? How can we use this information to understand the car's motion? Now, let's think about how we could apply similar reasoning to other scenarios, like analyzing the rate of change of population growth or the rate at which a chemical reaction occurs."

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |