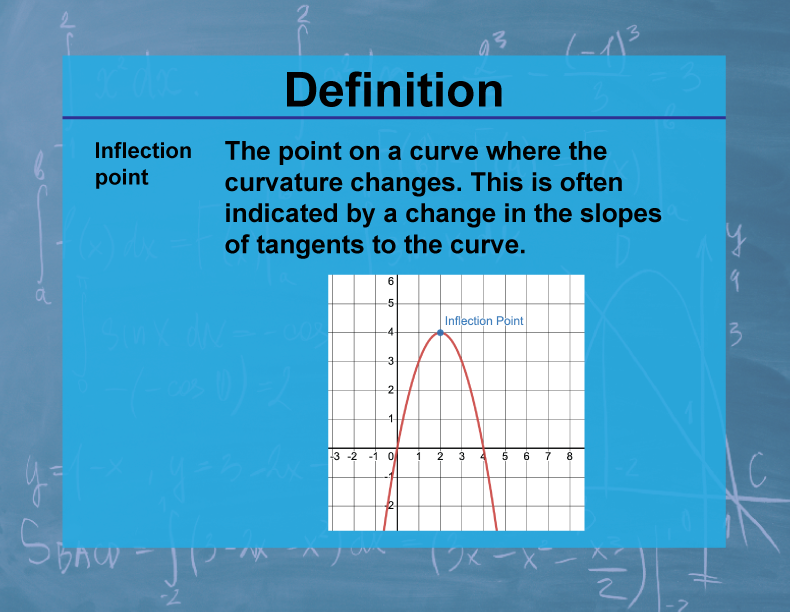
Definition--Calculus Topics--Inflection Point
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Advanced Topics in Algebra >> Calculus Vocabulary

Definition--Calculus Topics--Inflection Point

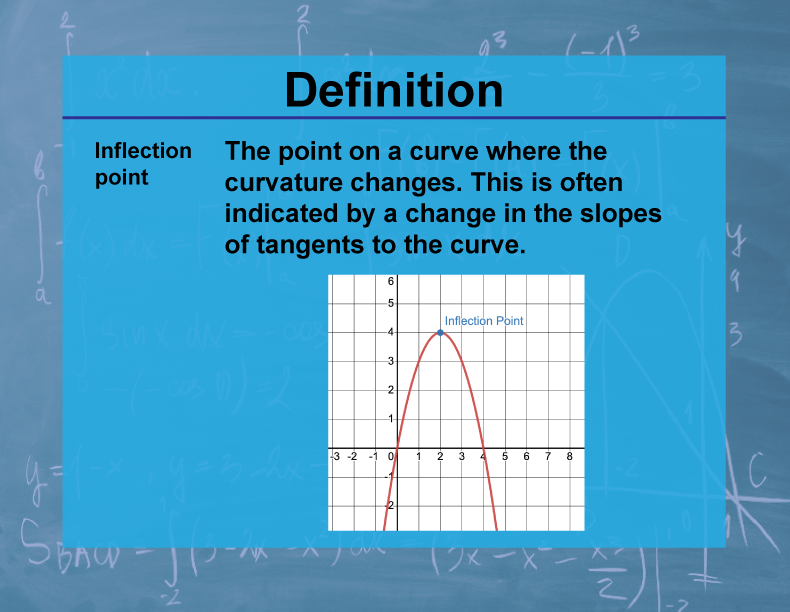
Definition--Calculus Topics--Inflection Point

The point on a curve where the curvature changes. This is often indicated by a change in the slopes of tangents to the curve.

— CLICK THE PREVIEW BUTTON TO SEE THE DEFINITION CARD —

To see the complete collection of Calculus terms, click on this link.

Common Core Standards CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C
Grade Range 11 - 12
Curriculum Nodes Algebra
    • Advanced Topics in Algebra
        • Calculus Vocabulary
Copyright Year 2023
Keywords calculus concepts, limits, derivatives, integrals, composite functions