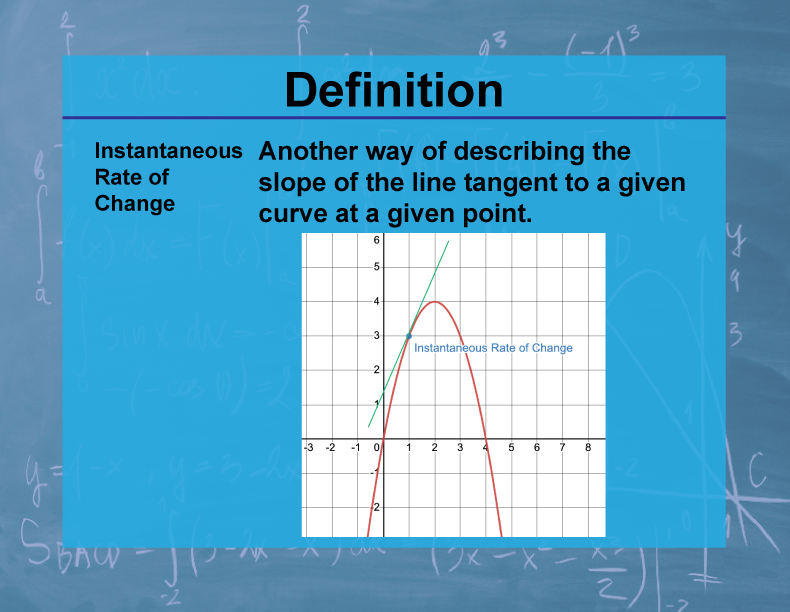
Definition--Calculus Topics--Instantaneous Rate of Change
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Advanced Topics in Algebra >> Calculus Vocabulary

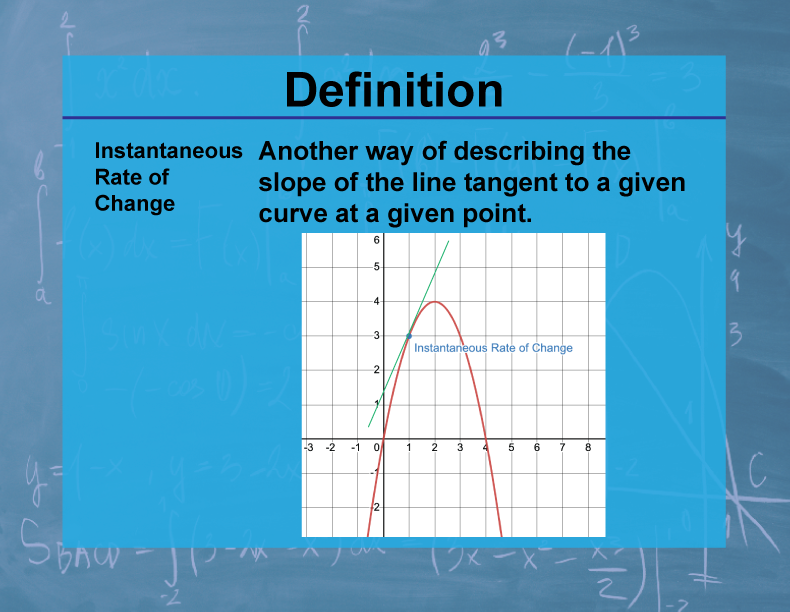
Definition--Calculus Topics--Instantaneous Rate of Change

Definition--Calculus Topics--Instantaneous Rate of Change

Another way of describing the slope of the line tangent to a given curve at a given point.

— CLICK THE PREVIEW BUTTON TO SEE THE DEFINITION CARD —

To see the complete collection of Calculus terms, click on this link.

Common Core Standards CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C
Grade Range 11 - 12
Curriculum Nodes Algebra
    • Advanced Topics in Algebra
        • Calculus Vocabulary
Copyright Year 2023
Keywords calculus concepts, limits, derivatives, integrals, composite functions