Display Title
Definition--Calculus Topics--Intermediate Value Theorem
Display Title
Definition--Calculus Topics--Intermediate Value Theorem
Topic
Calculus
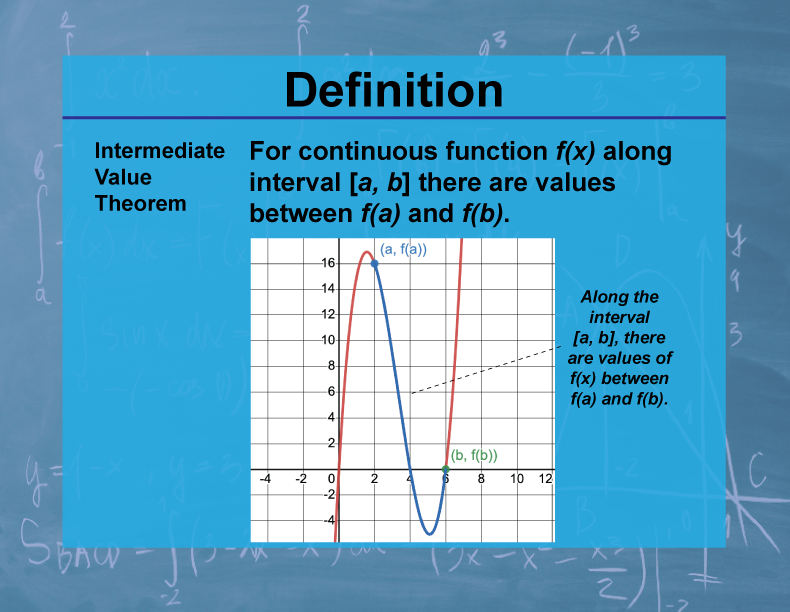
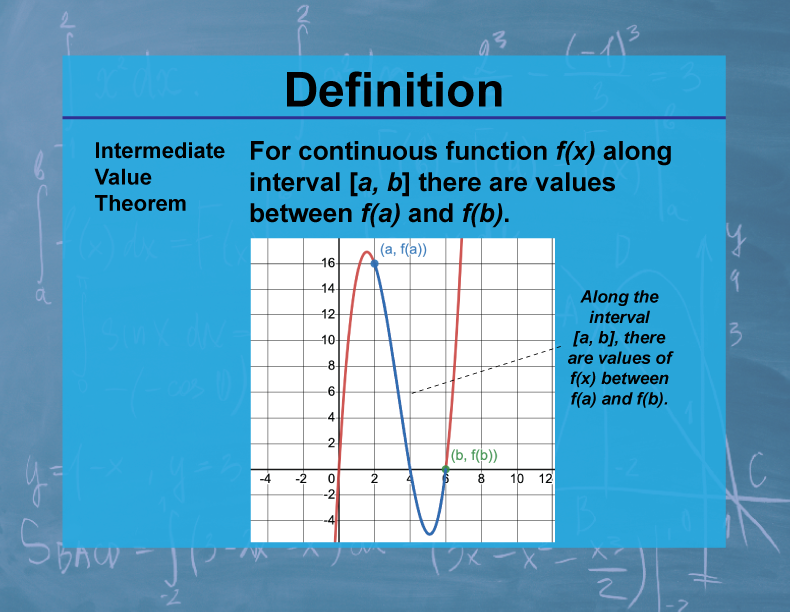
Definition
The Intermediate Value Theorem states that if f is a continuous function on the closed interval [a,b], and k is any value between f(a) and f(b), then there exists at least one c in [a,b] such that f(c) = k.
Description
The Intermediate Value Theorem is a fundamental result in calculus that guarantees the existence of solutions to certain equations. It has important applications in various fields, including physics, engineering, and economics. For example, it's used in numerical analysis to find roots of equations and in control theory to analyze system behavior.
In mathematics education, the Intermediate Value Theorem helps students develop intuition about continuous functions and their properties. It bridges the gap between algebraic and graphical representations of functions, encouraging students to visualize function behavior. This theorem is also crucial for understanding more advanced concepts in analysis and topology.
Teacher's Script: "Imagine you're hiking a continuous trail from sea level to the top of a mountain. The Intermediate Value Theorem tells us that you'll pass through every elevation between sea level and the peak at least once. Now, let's apply this to a function. If we have a continuous function f(x) on [0,5], and f(0) = -2 and f(5) = 3, can we guarantee that there's a point where f(x) = 0? Why? How could we use this theorem to prove the existence of solutions to equations like x3 - x - 1 = 0?"

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |