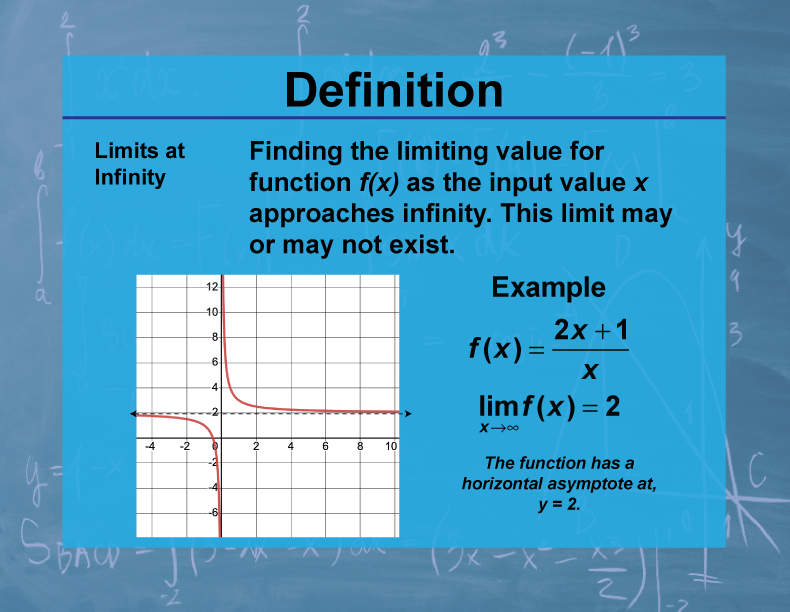
Definition--Calculus Topics--Limits at Infinity
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Advanced Topics in Algebra >> Calculus Vocabulary

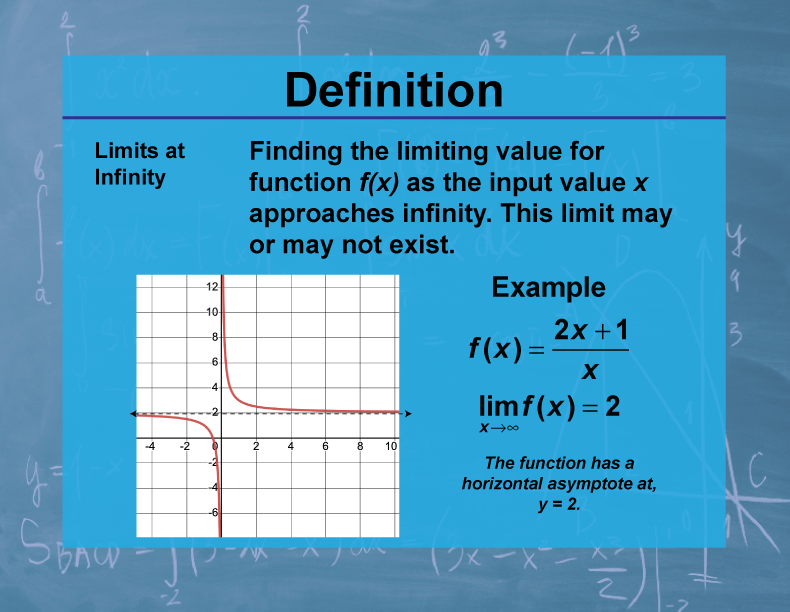
Definition--Calculus Topics--Limits at Infinity

Definition--Calculus Topics--Limits at Infinity

Finding the limiting value for function f(x) as the input value x approaches infinity. This limit may or may not exist.

— CLICK THE PREVIEW BUTTON TO SEE THE DEFINITION CARD —

To see the complete collection of Calculus terms, click on this link.

Common Core Standards CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C
Grade Range 11 - 12
Curriculum Nodes Algebra
    • Advanced Topics in Algebra
        • Calculus Vocabulary
Copyright Year 2023
Keywords calculus concepts, limits, derivatives, integrals, composite functions