
Display Title
Definition--Calculus Topics--Linear Approximation
Display Title
Definition--Calculus Topics--Linear Approximation

Topic
Calculus
Definition
A linear approximation of a function f(x) near a point x = a is given by the tangent line to the graph of f at the point (a, f(a)). The equation of this line is L(x) = f(a) + f'(a)(x - a), where f'(a) is the derivative of f at a.
Description
Linear approximation is a powerful tool in calculus that allows us to estimate function values using a simple linear function. It's based on the idea that any differentiable function looks approximately linear when zoomed in sufficiently close to a point. This concept has wide-ranging applications in physics, engineering, and economics, where it's often used to simplify complex systems for analysis.
In mathematics education, linear approximation helps students connect the concepts of derivatives and tangent lines to practical applications. It provides a concrete way to understand how derivatives can be used to estimate function values. This topic also introduces students to the idea of local linearity, which is fundamental to many advanced concepts in calculus and analysis.
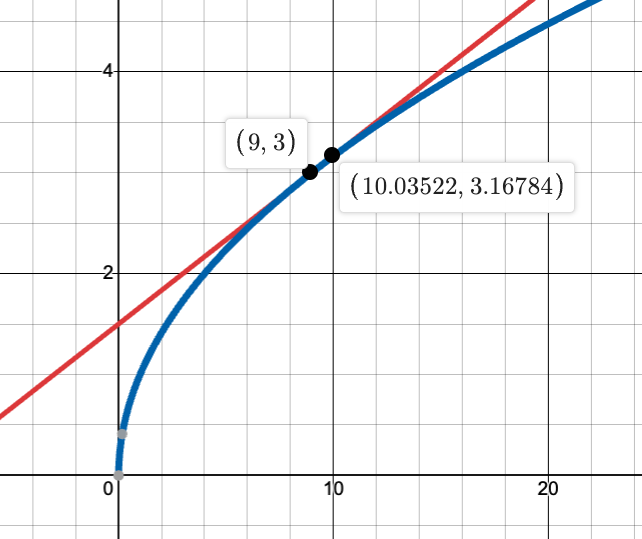
Teacher's Script: "Imagine you're trying to calculate the square root of 10. Instead of using a calculator, we can use a linear approximation. We know √9 = 3, so let's approximate √10 near x = 9 for the function is f(x) = √x. We want to find L(x) at a = 9. First, we calculate f'(x) = 1/(2√x). Now, let's work through setting up L(x) = f(9) + f'(9)(x - 9). How close does this get us to the actual value of √10? When might such an approximation be useful in real-world scenarios?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |