
Display Title
Definition--Calculus Topics--Local Minimum
Display Title
Definition--Calculus Topics--Local Minimum

Topic
Calculus
Definition
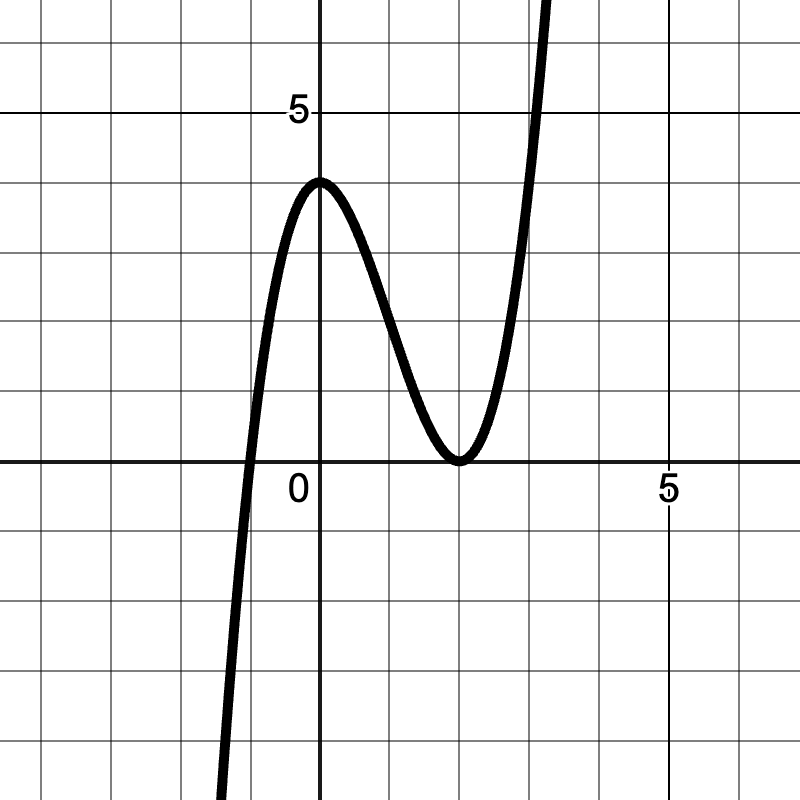
A local minimum of a function f(x) occurs at a point x = c if f(c) ≤ f(x) for all x in some open interval containing c. In other words, f(c) is the smallest value of the function in some neighborhood around c.
Description
Local minima are essential in understanding function behavior and are widely used in optimization problems across various fields. In economics, they might represent minimum costs or lowest points of inefficiency; in physics, they could indicate points of unstable equilibrium. Identifying local minima is often a key step in solving real-world problems involving minimization.
In mathematics education, the concept of local minima helps students develop a deeper understanding of function behavior. It's closely tied to the study of derivatives, as local minima often occur at points where the derivative is zero or undefined. This concept also introduces students to the idea that a function can have multiple "low points" without necessarily achieving a global minimum.
Teacher's Script: "Imagine you're designing a storage container. The local minima of the surface area function would represent designs that use less material than the designs 'nearby'. If we model the surface area as a function of the container's dimensions, how could we find these efficient designs mathematically? Let's look at the function f(x) = x3 - 3x2 + 4. How can we use derivatives to find its local minima? What does each step in this process tell us about the function's behavior? Can you think of other real-world scenarios where identifying local minima would be important?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |