Display Title
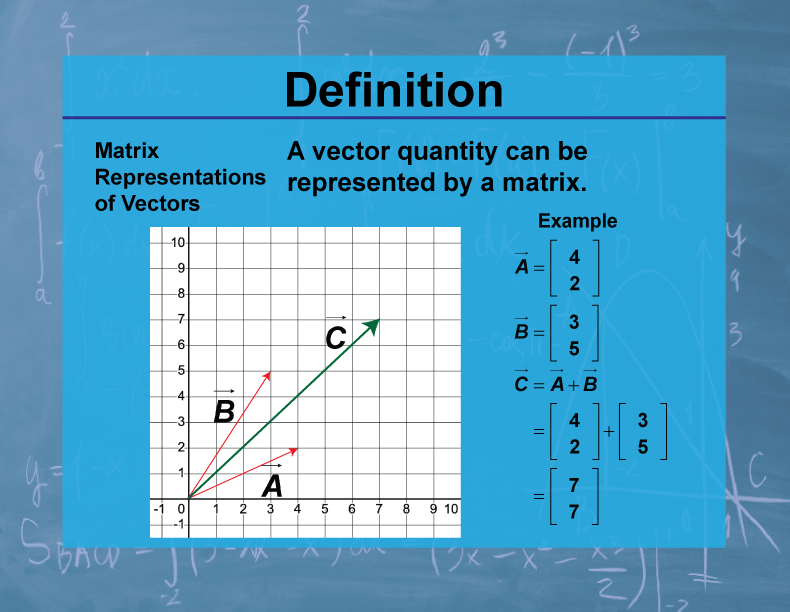
Definition--Calculus Topics--Matrix Representations of Vectors
Display Title
Definition--Calculus Topics--Matrix Representations of Vectors
Topic
Calculus
Definition
A matrix representation of a vector is a way to express a vector as a matrix, typically as a column matrix (n x 1) or a row matrix (1 x n).
Description
Matrix representations of vectors are fundamental in linear algebra and have important applications in calculus, particularly in multivariable calculus and vector calculus. They provide a convenient way to perform vector operations using matrix algebra. In physics and engineering, these representations are crucial for describing and analyzing systems with multiple variables or dimensions.
In mathematics education, understanding matrix representations of vectors helps students bridge the gap between geometric and algebraic thinking. It prepares them for more advanced topics in linear algebra and multivariable calculus. This concept also introduces students to the power of matrices in simplifying complex calculations and representing transformations.
Teacher's Script: "Let's consider a 3D vector v = (2, -1, 3). We can represent this as a column matrix [2; -1; 3] or a row matrix [2 -1 3]. How might we use these representations to perform vector operations? For example, if we want to scale this vector by 2, we can simply multiply each element of the matrix by 2. Or if we want to rotate this vector in 3D space, we can multiply it by a rotation matrix. Can you see how this representation makes these operations more systematic and easier to compute?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |