
Display Title
Definition--Calculus Topics--Mean Value Theorem
Display Title
Definition--Calculus Topics--Mean Value Theorem

Topic
Calculus
Definition
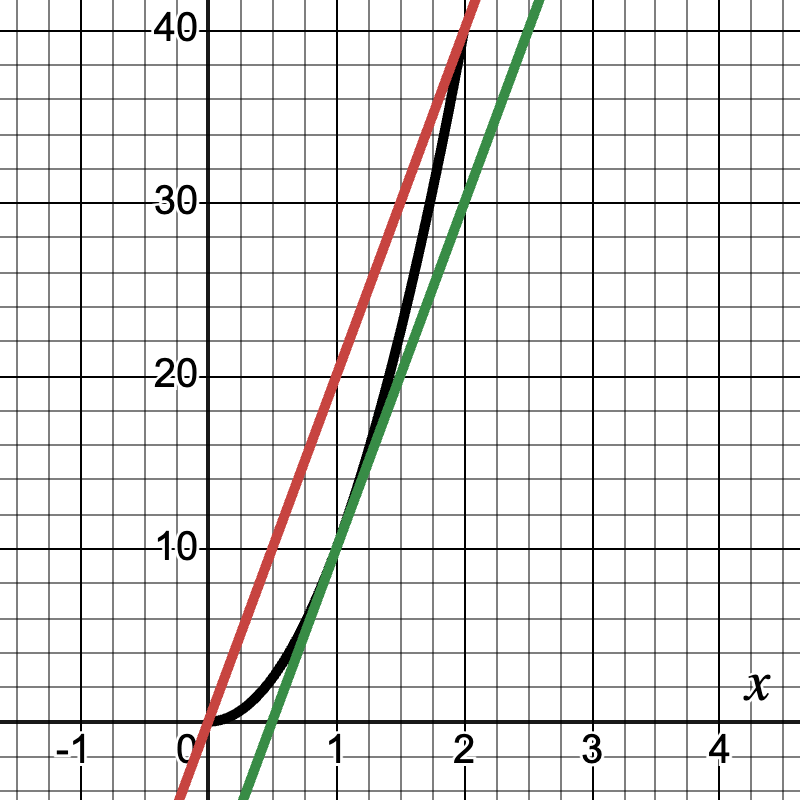
The Mean Value Theorem states that for a function f(x) that is continuous on [a,b] and differentiable on (a,b), there exists at least one c in (a,b) such that f'(c) = [f(b) - f(a)] / (b - a).
Description
The Mean Value Theorem is a fundamental result in calculus that connects the average rate of change of a function over an interval to its instantaneous rate of change at some point within that interval. It has important applications in both pure and applied mathematics, including optimization problems, approximation theory, and in proving other important theorems in calculus.
In mathematics education, the Mean Value Theorem helps students understand the relationship between average and instantaneous rates of change. It provides a powerful tool for analyzing function behavior and is crucial for developing intuition about derivatives. This theorem also serves as a bridge between differential and integral calculus, highlighting the deep connections within the subject.
Teacher's Script: "Imagine you're on a road trip. Your average speed for the entire journey is 20 mph. The Mean Value Theorem tells us that at some point during your trip, your speedometer must have read exactly 20 mph. Let's apply this to a function f(x) = 10x2 on the interval [0, 3]. Can we find a point where the instantaneous rate of change equals the average rate of change? How does this relate to the tangent line and secant line of the function? This theorem gives us a powerful way to analyze functions and their derivatives."
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |