Display Title
Definition--Calculus Topics--Oblique Asymptote
Display Title
Definition--Calculus Topics--Oblique Asymptote
Topic
Calculus
Definition
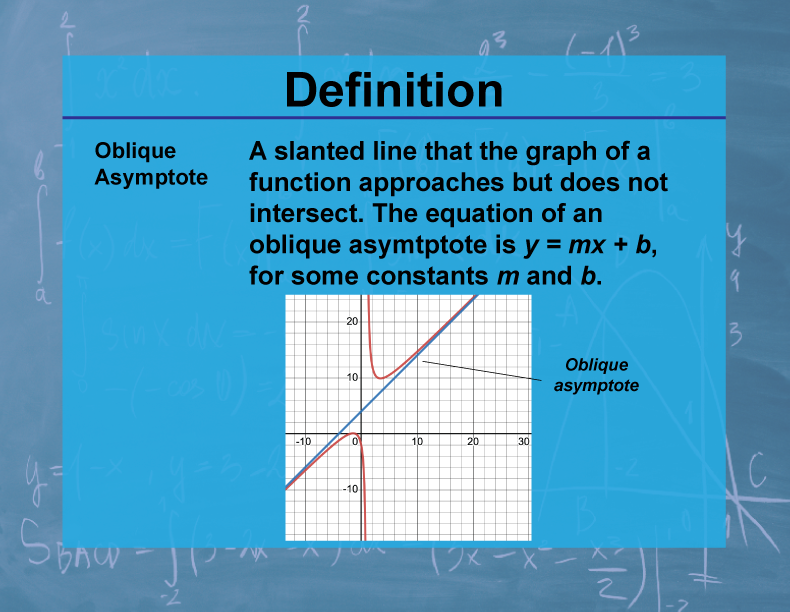
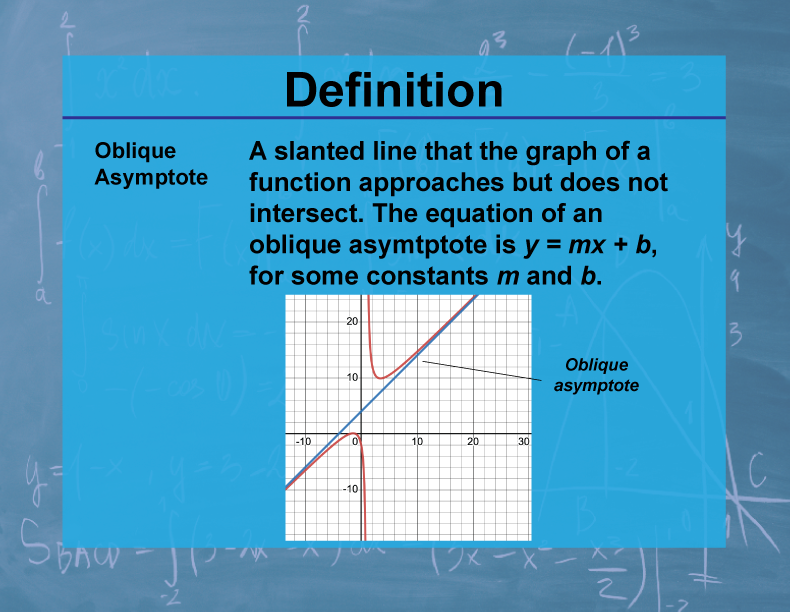
An oblique asymptote is a slanted line that a graph of a function approaches as x approaches positive or negative infinity. The equation of an oblique asymptote is typically of the form y = mx + b, where m ≠ 0.
Description
Oblique asymptotes are important in understanding the end behavior of certain functions, particularly rational functions where the degree of the numerator is exactly one more than the degree of the denominator. They provide crucial information about how a function behaves for very large or very small input values. In applied mathematics and sciences, oblique asymptotes can model phenomena that approach a linear trend over time or with increasing scale.
In mathematics education, the concept of oblique asymptotes helps students develop a deeper understanding of function behavior and limits. It bridges algebraic techniques (like polynomial long division) with graphical interpretation. This topic also prepares students for more advanced concepts in calculus and analysis, such as improper integrals and series.
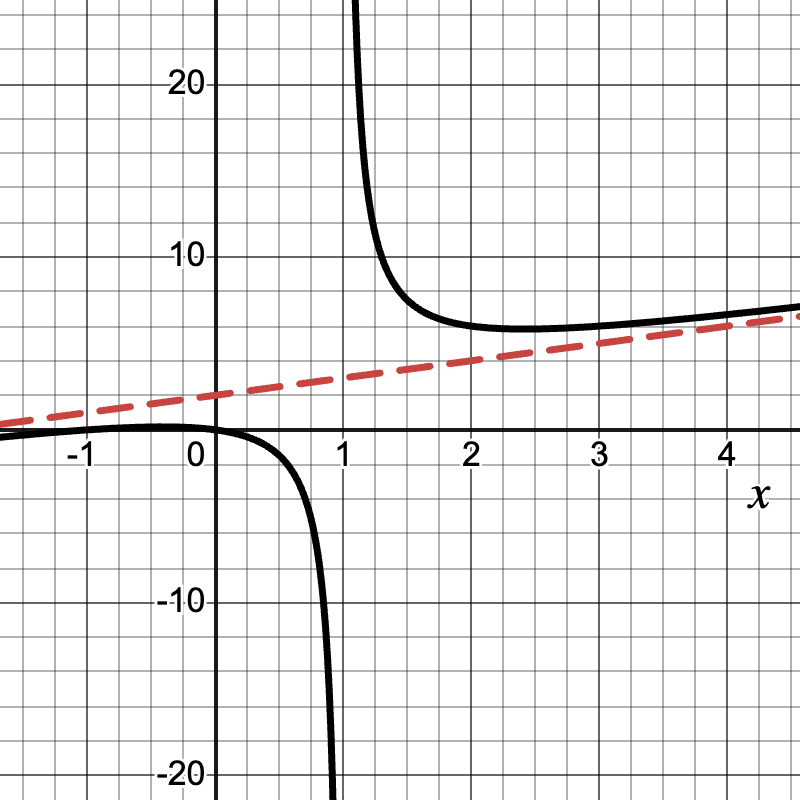
Teacher's Script: "Let's consider the function f(x) = (x2 + x) / (x - 1). How does this function behave as x gets very large? To find the oblique asymptote, we can use polynomial long division. The result gives us y = x + 2, which is our oblique asymptote. Now, let's graph this function and its asymptote. How does the function approach this line? Can you think of real-world scenarios where we might see this kind of behavior, perhaps in economics or physics?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |