
Display Title
Definition--Calculus Topics--One-Sided Limits
Display Title
Definition--Calculus Topics--One-Sided Limits

Topic
Calculus
Definition
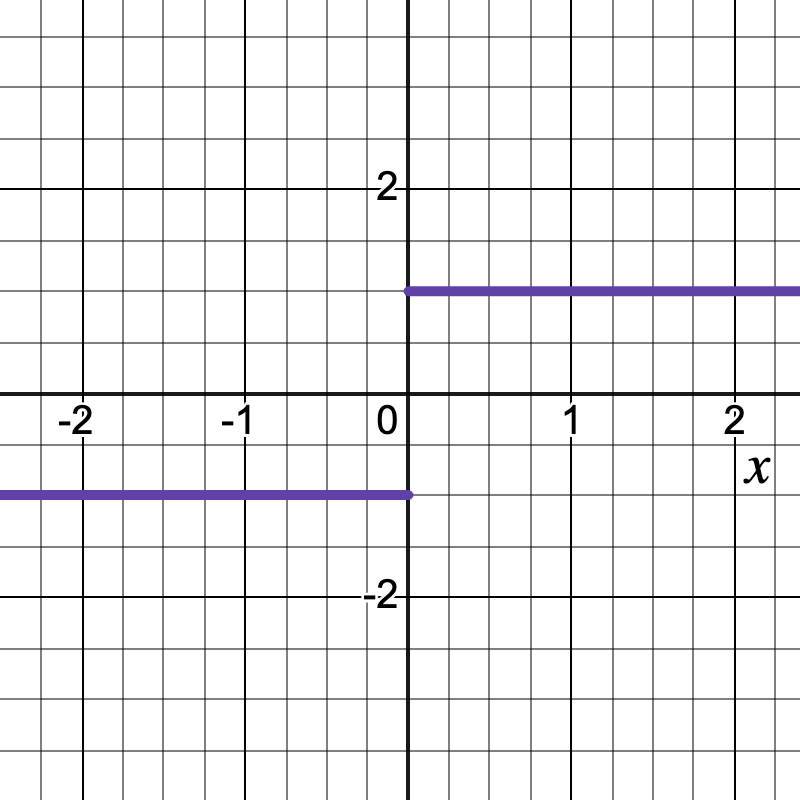
A one-sided limit is the value that a function approaches as the input approaches a specified value from either the left or the right. The left-hand limit is denoted as lim[x→a-] f(x), and the right-hand limit as lim[x→a+] f(x).
Description
One-sided limits are crucial in understanding function behavior, especially at points of discontinuity or where the function is defined differently on either side of a point. They are fundamental in analyzing piecewise functions, step functions, and in understanding continuity. In real-world applications, one-sided limits can model situations where a system's behavior just before or after a critical point is important.
In mathematics education, understanding one-sided limits helps students develop a more nuanced view of function behavior. It's particularly important for grasping the concept of continuity and preparing for more advanced topics in calculus. One-sided limits also introduce students to the idea that limits can exist even when a function is not defined at a point, broadening their understanding of mathematical analysis.
Teacher's Script: "Imagine you're analyzing the temperature of water as it's heated. As the temperature approaches 100°C, the water's behavior just before boiling might be different from its behavior just after. This is where one-sided limits come in handy. Let's look at a mathematical example: f(x) = |x| / x. What happens as x approaches 0 from the positive side? From the negative side? How do these one-sided limits help us understand the behavior of this function at x = 0? Can you think of other real-world scenarios where we might need to consider what happens 'just before' or 'just after' a critical point?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |