Display Title
Definition--Calculus Topics--Riemann Sum
Display Title
Definition--Calculus Topics--Riemann Sum
Topic
Calculus
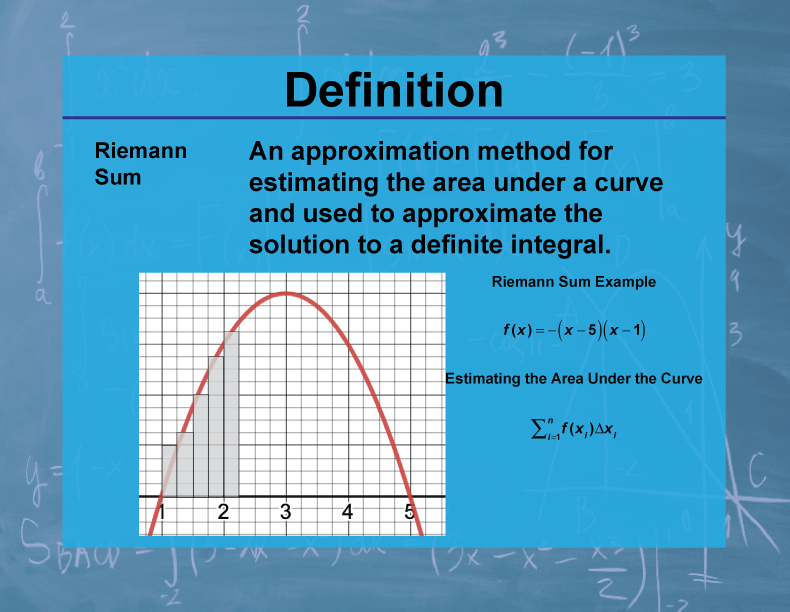
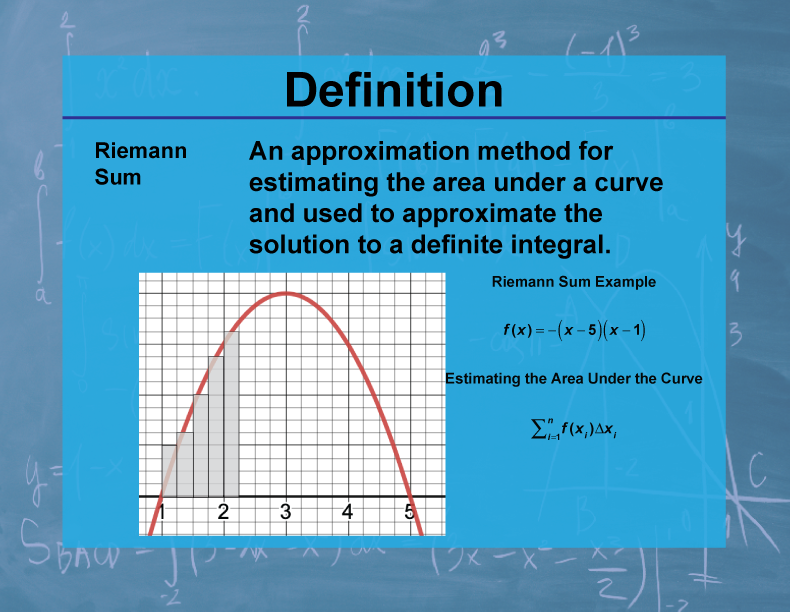
Definition
A Riemann sum is a method of approximating the area under a curve by dividing it into rectangles and summing their areas. The sum is of the form Σf(x*i)Δx, where f(x*i) is the function value at a chosen point in each subinterval and Δx is the width of each rectangle.
Description
Riemann sums are fundamental to the development of the definite integral in calculus. They provide a concrete way to understand the concept of area under a curve and serve as a bridge between discrete summation and continuous integration. Riemann sums come in various forms (left, right, midpoint, trapezoidal) and are crucial for numerical integration techniques.
In mathematics education, Riemann sums help students visualize the process of integration and understand the relationship between area and summation. They provide an intuitive foundation for the Fundamental Theorem of Calculus and help students appreciate the power of limits in defining precise mathematical concepts. Riemann sums also introduce students to the idea of approximation and error in mathematical calculations.
Teacher's Script: "Let's approximate the area under the curve y = x2 from x = 0 to x = 2 using four rectangles. We'll use left endpoints for our function values. Can you calculate the height and width of each rectangle? Now, sum up their areas. How close do you think this is to the actual area? How might our approximation change if we use right endpoints or midpoints instead? This process helps us understand how integration 'adds up' infinitely many infinitesimally small rectangles to find exact areas."
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |