Display Title
Definition--Calculus Topics--Rolle's Theorem
Display Title
Definition--Calculus Topics--Rolle's Theorem
Topic
Calculus
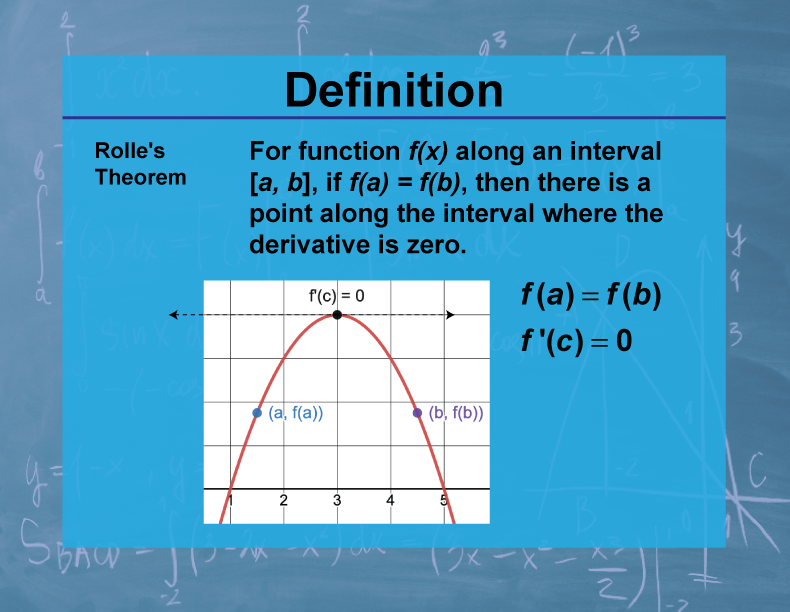
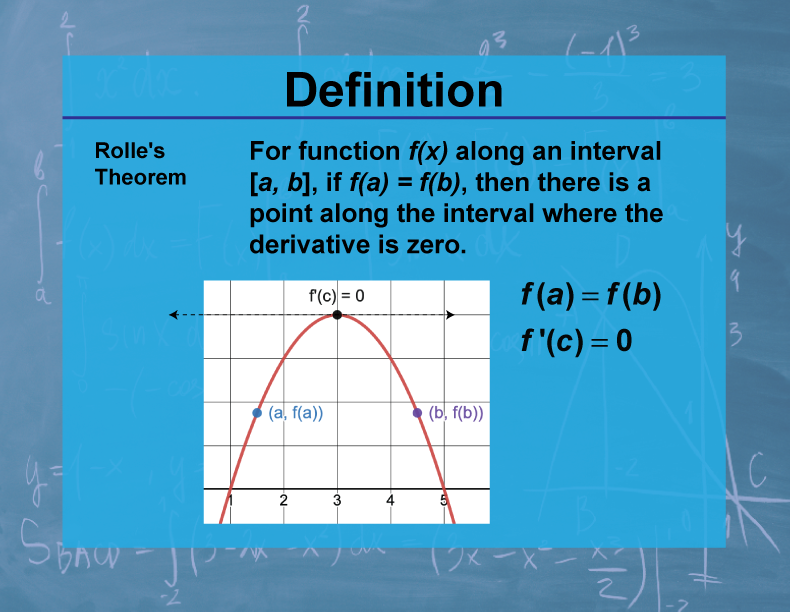
Definition
Rolle's Theorem states that for a function f(x) that is continuous on [a,b] and differentiable on (a,b), if f(a) = f(b), then there exists at least one c in (a,b) such that f'(c) = 0.
Description
Rolle's Theorem is a fundamental result in calculus that provides insight into the behavior of functions. It essentially states that if a continuous function takes the same value at two distinct points, there must be a point between them where the function's derivative is zero. This theorem has important applications in optimization problems and in proving other key theorems in calculus, such as the Mean Value Theorem.
In mathematics education, Rolle's Theorem helps students understand the relationship between a function's values and its rate of change. It provides a powerful tool for analyzing function behavior and is crucial for developing intuition about derivatives. This theorem also serves as a bridge between the concepts of continuity and differentiability, highlighting the deep connections within calculus.
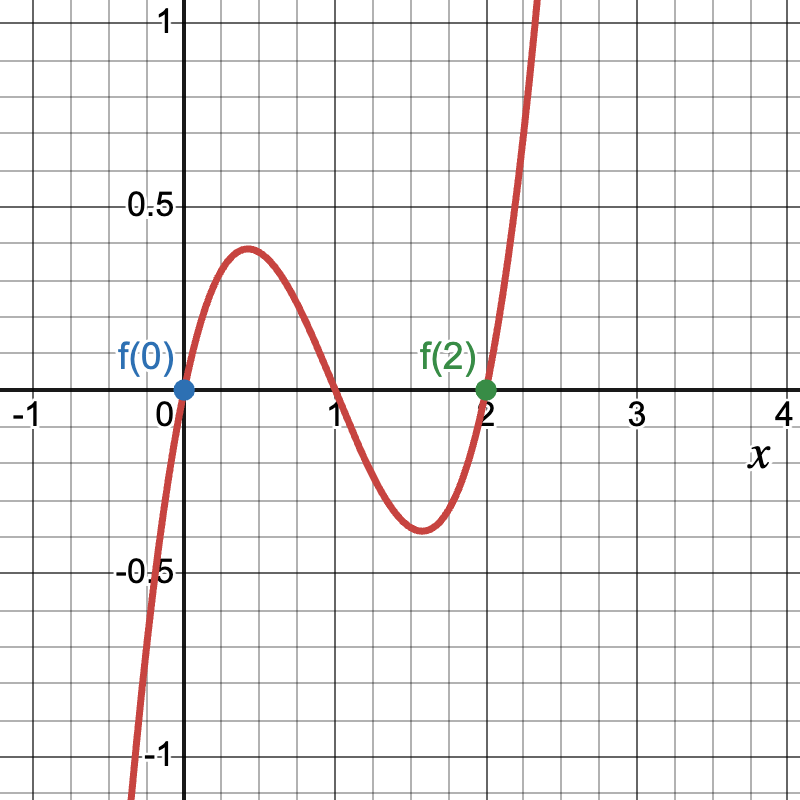
Teacher's Script: "Imagine you're hiking a trail that starts and ends at the same elevation. Rolle's Theorem guarantees that at some point on your hike, you'll be walking on level ground (zero slope). Let's apply this to a function, say f(x) = x3 - 3x2 + 2x on the interval [0,2]. Can we show that f(0) = f(2)? If so, Rolle's Theorem tells us there must be a point c between 0 and 2 where f'(c) = 0. Can you find this point? How does this relate to the graph of the function?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |