Display Title
Definition--Calculus Topics--Second Derivative
Display Title
Definition--Calculus Topics--Second Derivative
Topic
Calculus
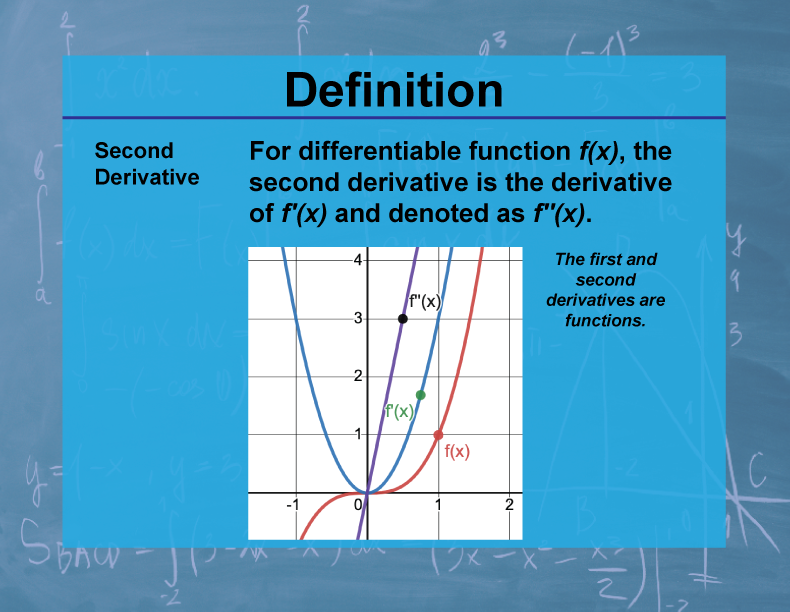
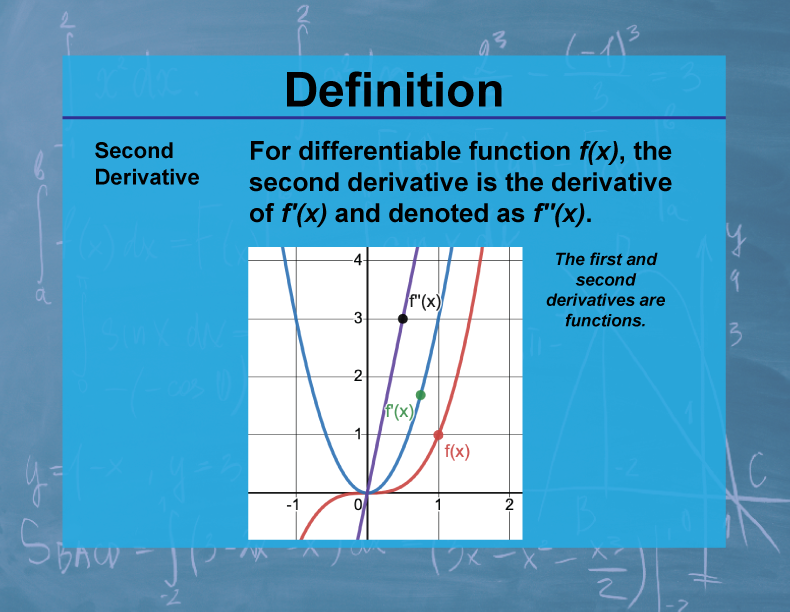
Definition
The second derivative of a function f(x), denoted as f''(x), is the derivative of the derivative of f(x). It represents the rate of change of the rate of change of the original function.
Description
The second derivative is a crucial concept in calculus, providing information about the curvature and concavity of functions. In physics, it often represents acceleration when the original function describes position. The second derivative is used to identify inflection points, determine the nature of critical points (maxima, minima), and analyze the behavior of functions in various fields including physics, engineering, and economics.
In mathematics education, understanding the second derivative helps students develop a deeper insight into function behavior. It's essential for analyzing graphs, solving optimization problems, and understanding concepts like concavity and inflection points. The second derivative also plays a key role in Taylor series expansions and in solving differential equations.
Teacher's Script: "Imagine you're analyzing the motion of a roller coaster. The position function s(t) gives the coaster's location at time t. The first derivative, s'(t), gives the velocity. Now, the second derivative, s''(t), gives the acceleration. How does this help us understand the ride? Where is the coaster speeding up or slowing down? Where are the thrilling moments of the ride? Let's graph these functions and see how they relate to each other and to the actual shape of the roller coaster track."

For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |