Display Title
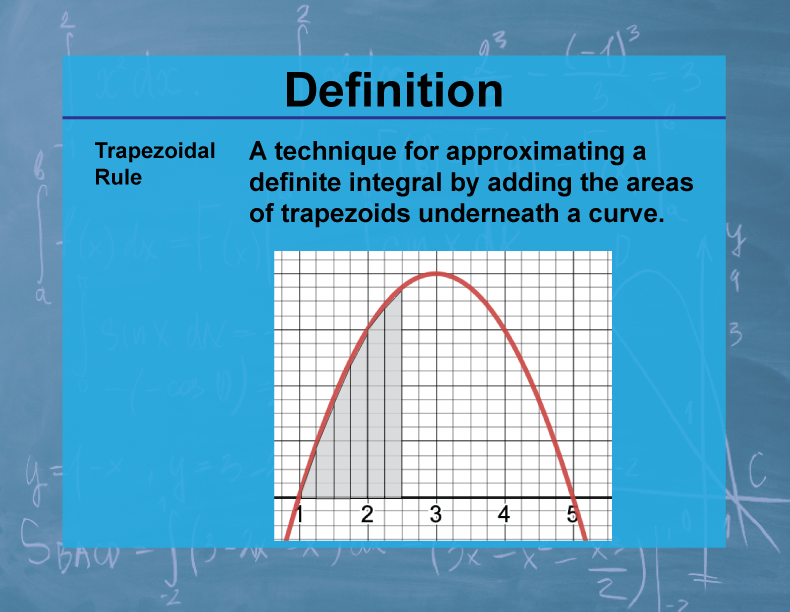
Definition--Calculus Topics--Trapezoidal Rule
Display Title
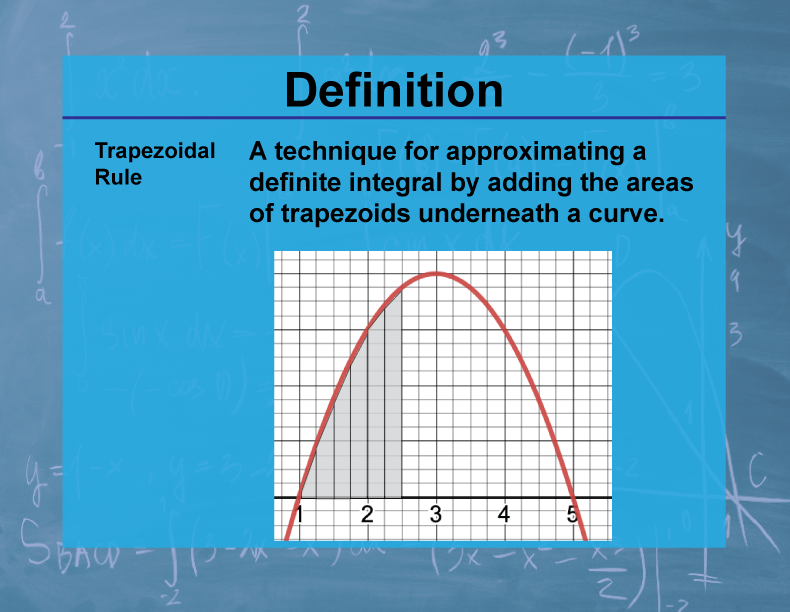
Definition--Calculus Topics--Trapezoidal Rule
Topic
Calculus
Definition
The Trapezoidal Rule is a method for approximating the definite integral of a function by dividing the area under the curve into trapezoids and summing their areas. For a function f(x) on the interval [a,b] divided into n subintervals, the approximation is given by: ∫[a to b] f(x)dx ≈ (Δx/2)[f(x₀) + 2f(x₁) + 2f(x₂) + ... + 2f(xₙ₋₁) + f(xₙ)], where Δx = (b-a)/n.
Description
The Trapezoidal Rule is an important numerical integration technique in calculus. It provides a way to estimate the area under a curve when analytical integration is difficult or impossible. This method is widely used in various fields of science and engineering for approximating integrals in practical applications. The Trapezoidal Rule is often more accurate than the simpler Rectangle Rule and serves as a stepping stone to more advanced numerical integration methods.
In mathematics education, the Trapezoidal Rule helps students understand the connection between geometry and calculus. It provides a concrete, visual method for approximating integrals, making the concept more accessible. This rule also introduces students to the idea of numerical approximation in calculus, preparing them for more advanced computational methods and error analysis.
Teacher's Script: "Imagine we're trying to calculate the area of a lake from a topographic map. We could divide the lake into strips and approximate each strip as a trapezoid. This is essentially what the Trapezoidal Rule does for functions. Let's apply this to approximate the integral of f(x) = x² from 0 to 2 using 4 subintervals. How close is our approximation to the actual value? How might increasing the number of subintervals affect our accuracy? This method gives us a powerful tool for estimating integrals when exact solutions are hard to find."
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |