Display Title
Definition--Calculus Topics--Trigonometric Function
Display Title
Definition--Calculus Topics--Trigonometric Function
Topic
Calculus
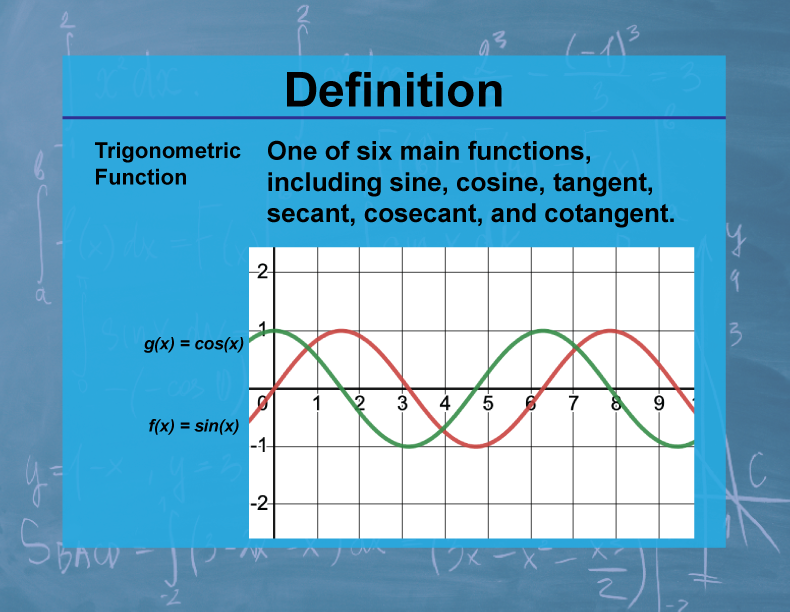
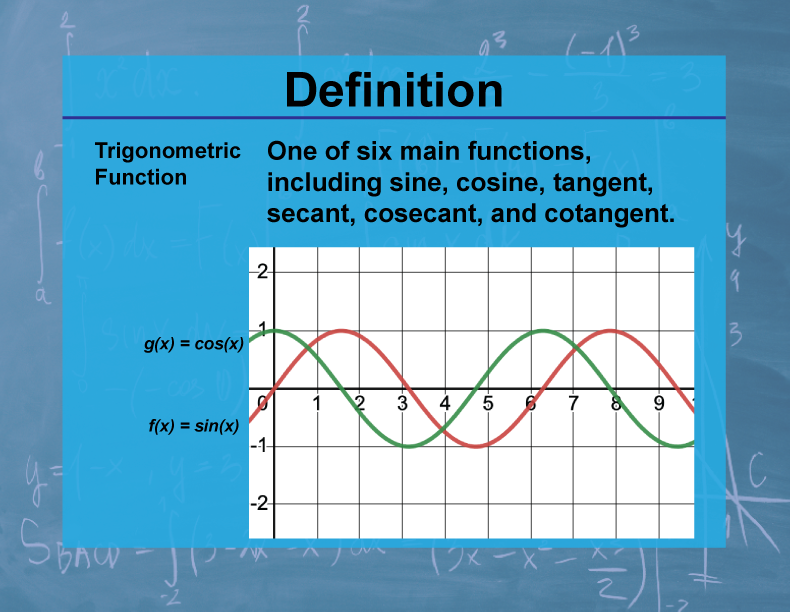
Definition
Trigonometric functions are functions of an angle and are fundamental in the study of triangles and periodic phenomena. The main trigonometric functions are sine, cosine, tangent, cotangent, secant, and cosecant.
Description
Trigonometric functions play a crucial role in calculus and have wide-ranging applications in physics, engineering, and other sciences. They are particularly useful for modeling periodic phenomena such as waves, oscillations, and circular motion. In calculus, understanding the derivatives and integrals of trigonometric functions is essential for solving many types of problems and differential equations.
In mathematics education, trigonometric functions serve as a bridge between geometry and analysis. They introduce students to the concept of periodic functions and provide a concrete example of functions that cannot be expressed as simple algebraic expressions. Learning about trigonometric functions also prepares students for more advanced topics in calculus, such as Fourier series and complex analysis.
Teacher's Script: "Imagine you're analyzing the motion of a pendulum. The angle of the pendulum from its equilibrium position can be modeled by a sine function: θ(t) = A sin(ωt), where A is the amplitude and ω is the angular frequency. How would we find the velocity and acceleration of the pendulum? This involves differentiating the sine function. Can you think of other real-world phenomena that might be modeled using trigonometric functions? Understanding these functions and their properties is crucial for many applications in science and engineering."
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |