Display Title
Definition--Calculus Topics--Vertical Asymptote
Display Title
Definition--Calculus Topics--Vertical Asymptote
Topic
Calculus
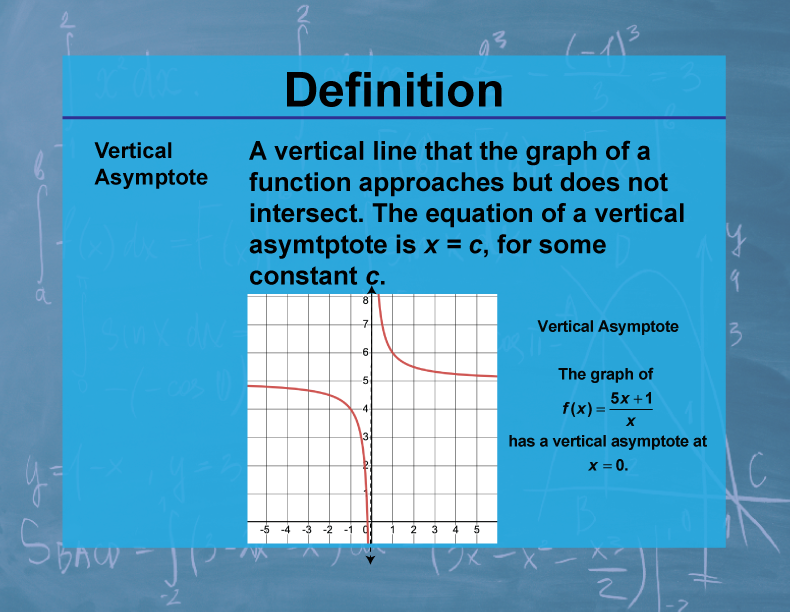
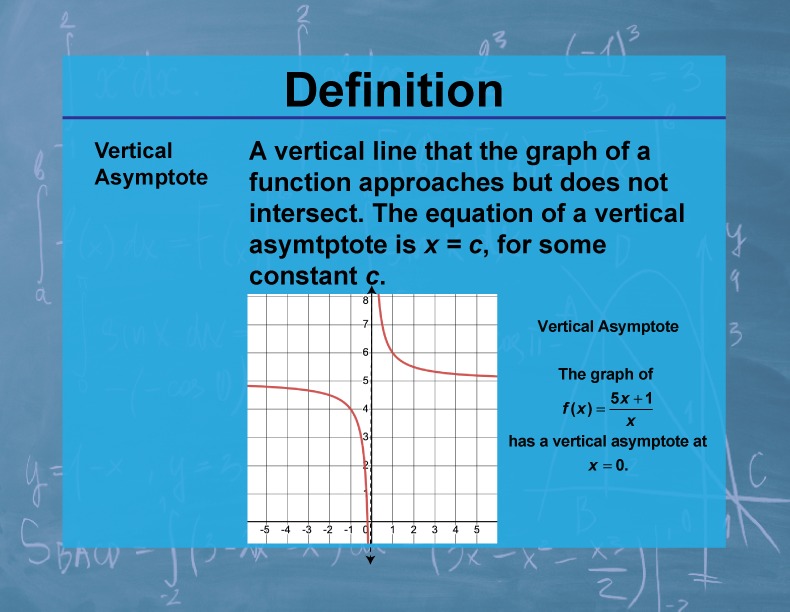
Definition
A vertical asymptote is a vertical line x = a to which the graph of a function f(x) approaches as x approaches a from either the left or right, but f(a) is undefined or the limit of f(x) as x approaches a is infinite.
Description
Vertical asymptotes are crucial in understanding the behavior of functions, particularly rational functions and functions with singularities. They indicate points where a function's values grow arbitrarily large in magnitude. In calculus, vertical asymptotes are important for analyzing limits, continuity, and the overall shape of function graphs.
In mathematics education, the concept of vertical asymptotes helps students develop a deeper understanding of function behavior and limits. It challenges students to think about what happens to a function as it approaches certain critical points. This concept is particularly important in preparing students for more advanced topics in calculus and analysis, such as improper integrals and complex analysis.
Teacher's Script: "Let's consider the function f(x) = 1 / (x - 2). What happens as x gets very close to 2? The function values grow extremely large, either positive or negative. This is a vertical asymptote at x = 2. How would we graph this? Why can't the function cross this line? Can you think of real-world scenarios where we might encounter this kind of behavior, perhaps in physics or economics? Understanding vertical asymptotes helps us analyze and predict the behavior of many important functions and models."
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |