Display Title
Definition--Calculus Topics--Zeros of a Function
Display Title
Definition--Calculus Topics--Zeros of a Function
Topic
Calculus
Definition
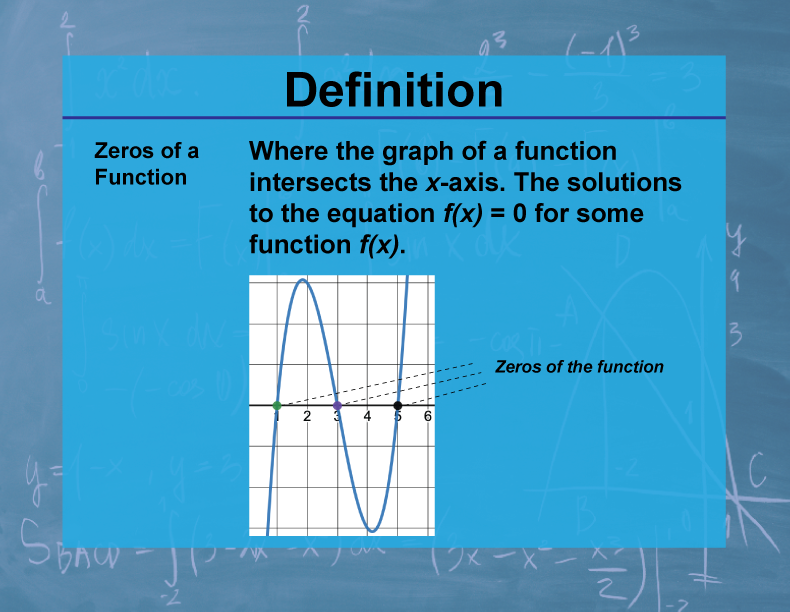
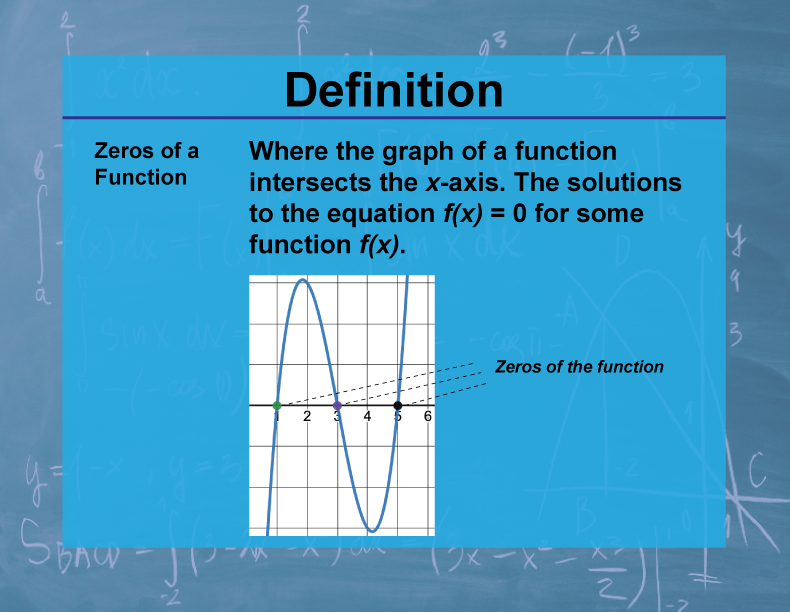
The zeros or roots of a function f(x) are the values of x for which f(x) = 0. Graphically, these are the x-coordinates of the points where the graph of the function crosses the x-axis.
Description
Understanding the zeros of a function is crucial in calculus and many areas of mathematics and science. Zeros provide important information about a function's behavior, including its sign changes and x-intercepts. In calculus, finding zeros is often a key step in solving optimization problems, analyzing function behavior, and solving differential equations.
In mathematics education, the concept of zeros helps students connect algebraic and graphical representations of functions. It reinforces the relationship between equations and their graphical solutions. Understanding zeros is also fundamental to more advanced topics in calculus, such as the Fundamental Theorem of Algebra and techniques for approximating solutions to equations.
Teacher's Script: "Let's consider the function f(x) = x2 - 4. To find its zeros, we solve the equation x2 - 4 = 0. We get x = ±2. What does this tell us about the graph? It crosses the x-axis at -2 and 2. Now, think about a real-world scenario, like a projectile motion where y = -4.9t2 + 20t represents the height of an object after t seconds. Finding the zeros of this function would tell us when the object hits the ground. Can you solve this? How does understanding zeros help us analyze and predict real-world phenomena?"
For a complete collection of terms related to Calculus click on this link: Calculus Vocabulary Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1.C |
|---|---|
| Grade Range | 11 - 12 |
| Curriculum Nodes |
Algebra • Advanced Topics in Algebra • Calculus Vocabulary |
| Copyright Year | 2023 |
| Keywords | calculus concepts, limits, derivatives, integrals, composite functions |