Display Title
Definition--Circle Concepts--Incenter of a Triangle
Display Title
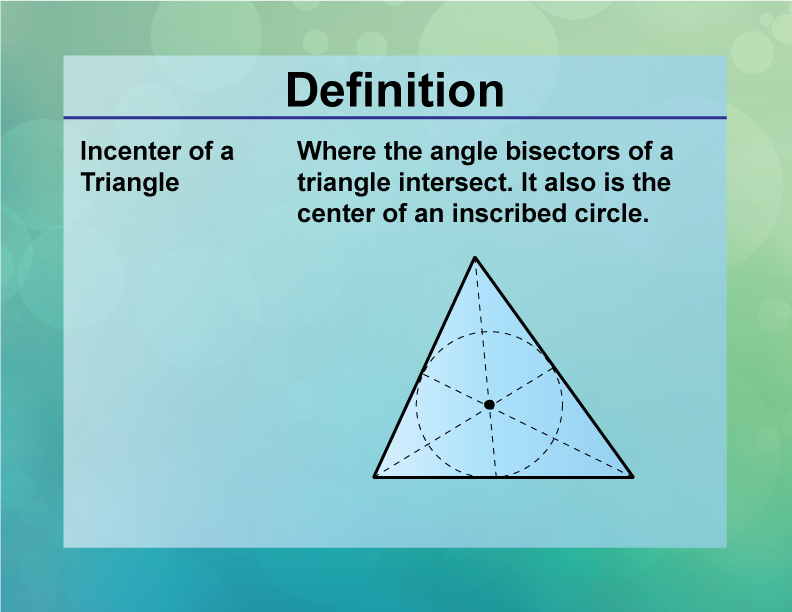
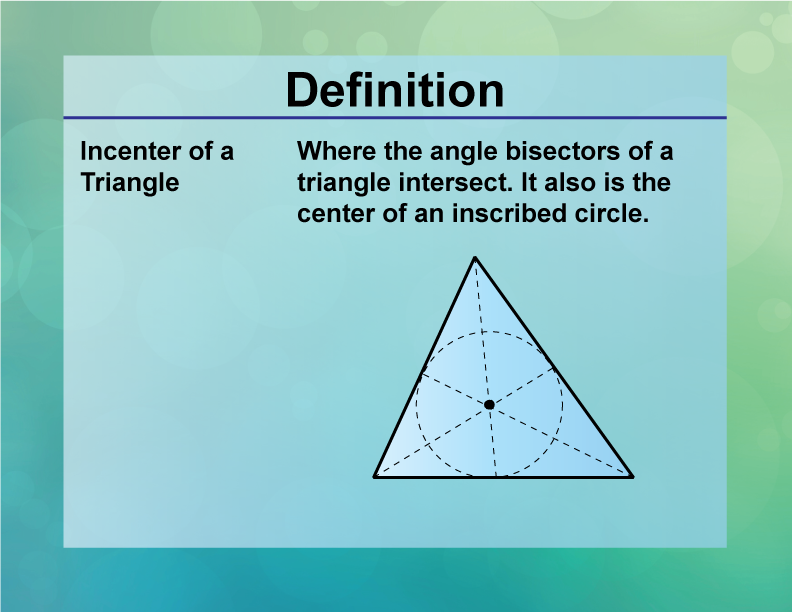
Incenter of a Triangle
Topic
Circles
Definition
The incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides.
Description
The incenter is a significant concept in geometry, representing the center of the incircle, the largest circle that fits within the triangle. This point is used in various applications, such as optimizing material usage in manufacturing and understanding natural phenomena like soap bubbles. In mathematics, the incenter is explored in the context of triangle properties and circle theorems, providing insights into geometric relationships. In education, understanding the incenter helps students develop problem-solving skills and geometric intuition, which are essential for advanced studies in geometry and trigonometry.

For a complete collection of terms related to Circles click on this link: Circles Collection.
| Common Core Standards | CCSS.MATH.CONTENT.HSG.C.A.2, CCSS.MATH.CONTENT.HSG.C.A.1, CCSS.MATH.CONTENT.HSG.C.A.3, CCSS.MATH.CONTENT.HSG.C.A.4, CCSS.MATH.CONTENT.4.MD.C.5.A, CCSS.MATH.CONTENT.7.G.B.4 |
|---|---|
| Grade Range | 4 - 8 |
| Curriculum Nodes |
Geometry • Circles • Definition of a Circle |
| Copyright Year | 2021 |
| Keywords | defnitions, geometry, circle |