edcom-728x90

IXL Ad

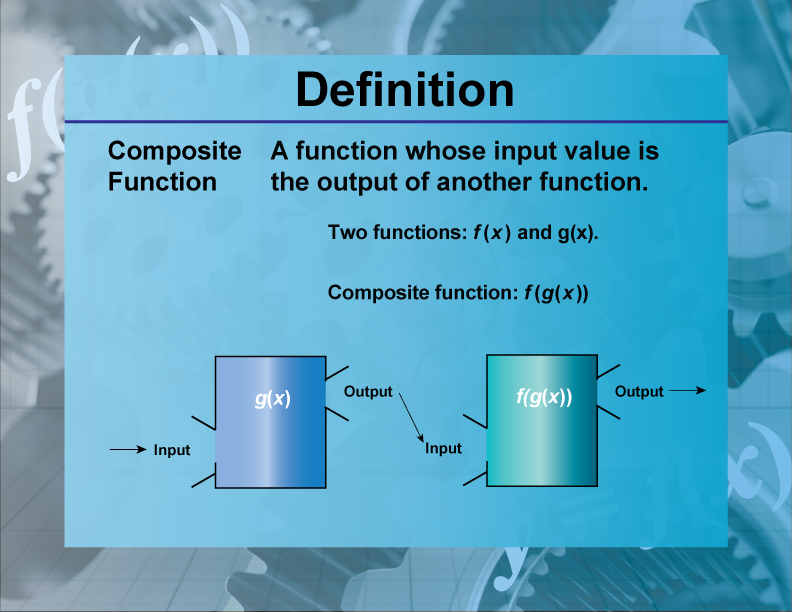
Definition--Functions and Relations Concepts--Composite Function
Register to SaveSubscribe to DownloadPreview Add to Slideshow
(Subscribers Only)

If you are a subscriber, please log in.

Algebra >> Functions and Relations >> Composite Functions

Definition--Functions and Relations Concepts--Composite Function

Composite Function

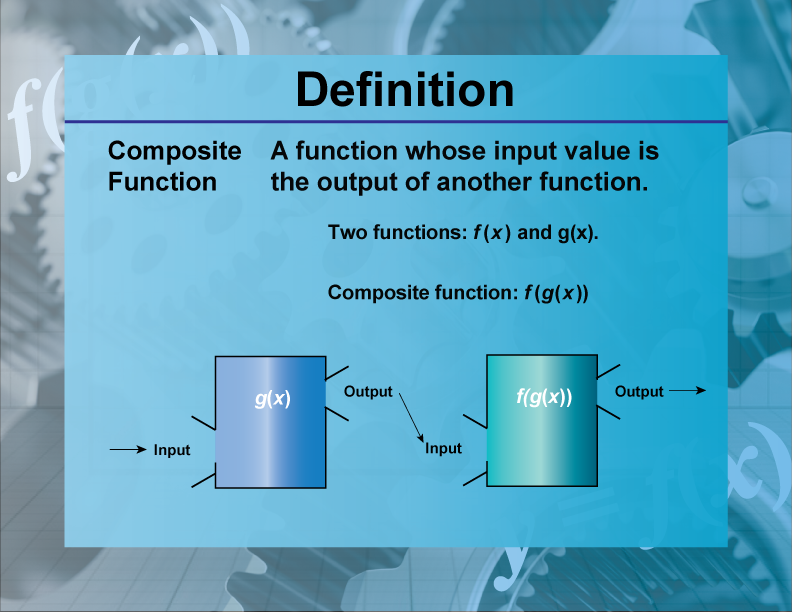
Composite Function Image

Topic

Functions and Relations

Definition

A composite function is a function that is formed when one function is applied to the result of another function.

Description

Composite functions are significant in mathematics because they allow the combination of two functions to form a new function. This is denoted as (f∘g)(x) = f(g(x)). Composite functions are widely used in various fields, including computer science for function composition in programming and in calculus for chain rule applications. For example, if f(x) = 2x and g(x) = x + 3, then the composite function 

(f∘g)(x) = f(g(x)) = 2(x + 3) = 2x+6

Understanding composite functions is crucial for solving complex mathematical problems and for the analysis of functions in higher mathematics.

For a complete collection of terms related to functions and relations click on this link: Functions and Relations Collection

Common Core Standards CCSS.MATH.CONTENT.8.F.A.1, CCSS.MATH.CONTENT.8.F.B.5, CCSS.MATH.CONTENT.HSF.IF.A.1, CCSS.MATH.CONTENT.HSF.IF.A.2, CCSS.MATH.CONTENT.HSF.IF.C.7, CCSS.MATH.CONTENT.HSF.BF.A.1, CCSS.MATH.CONTENT.HSF.BF.B.3, CCSS.MATH.CONTENT.HSF.BF.B.4
Grade Range 6 - 9
Curriculum Nodes Algebra
    • Functions and Relations
        • Composite Functions
Copyright Year 2021
Keywords definition, function, relations, glossary terms